Оценка параметров модели и влияние мультиколлинеарности факторов

Линейная регрессия сводится к нахождению параметров уравнения вида:

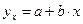(1)

Уравнение вида (1) позволяет по заданным фактическим значениям фактора x найти теоретические значения результативного признака.

Классический подход к оцениванию параметров линейной регрессии основан на методе наименьших квадратов (МНК). Система нормальных уравнений для оценки параметров a и b имеет следующий вид:

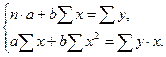(2)

Также параметры a и b можно рассчитать с помощью следующих формул:

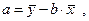
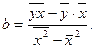(3)

C помощью корреляционно-регрессионного анализа можно получить оценки параметров уравнения. В качестве оценки статистической значимости результатов парной регрессии и корреляции могут выступать: значения F-критерия Фишера и t-критерия Стьюдента.

Оценка значимости уравнения регрессии в целом дается с помощью F-критерия Фишера. При этом выдвигается нулевая гипотеза H₀, что коэффициент регрессии равен нулю, т. е. b =0, и, следовательно, фактор x не оказывает влияния на результат. Значение F-критерия Фишера найдем по формуле:

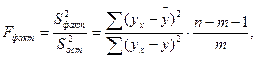(4)

где F_факт – критерий Фишера для проверки нулевой гипотезы H_о. Если F_факт> F_кр, то Н₀ отклоняется и уравнение считается статистически значимым в целом при соответствующем уровне значимости a. Если F_факт< F_кр, то Н₀ не может быть отклонена без серьезного риска сделать неправильный вывод о наличии связи. В этом случае с вероятностью p=1-a уравнение регрессии считается статистически незначимым и, скорее всего, связь между признаками случайна.

Величина F-критерия связана с линейным показателем детерминации (r²). Можно показать, что значение F-критерия равно:

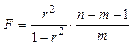(5)

Для оценки отдельных параметров уравнения определяется стандартная ошибка этих параметров. Формула стандартной ошибки для параметра b:

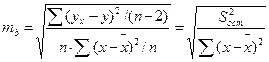(6)

где S²_ост – остаточная дисперсия на одну степень свободы.

Стандартная ошибка параметра а определяется по формуле:

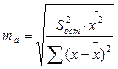(7)

Значимость линейного коэффициента корреляции проверяется на основе величины ошибки коэффициента корреляции m_r:

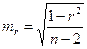(8)

Величина стандартной ошибки совместно с t-распределением Стьюдента при n-2 степенях свободы применяется для проверки существенности коэффициента регрессии. Для оценки существенности параметров и коэффициента корреляции их значения сравниваются со стандартной ошибкой, т. е. определяется фактическое значение t-критерия Стьюдента:

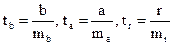(9)

Фактическое значение критерия сравнивается с табличным (критическим) при определенном уровне значимости a и числе степеней свободы n-2. Если t_факт> t_кр, то гипотезу о не существенности параметра регрессии и равенстве его нулю можно отклонить, а сам параметр является статистически значимым. Если t_факт< t_кр, то нулевая гипотеза Н₀ принимается с вероятностью 1-a и параметр статистически незначим.[4]

Линейное уравнение множественной регрессии имеет вид:

y=a+b₁x₁+b₂x₂+…+b_nx_n, (10)

где a, b₁, b₂…b_n – параметры уравнения; х₁, х₂…х_n – факторы, объясняющие переменные; у – результативный признак, зависимая переменная.

Параметры уравнения множественной регрессии оцениваются, как и в парной регрессии, методом наименьших квадратов (МНК):

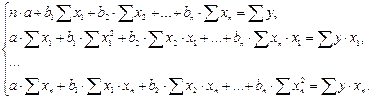(11)

Для ее решения можно применить обычный метод подстановок или воспользоваться методом определителей.

Значимость уравнения множественной регрессии в целом, так же как и в парной регрессии, оценивается с помощью F-критерия Фишера[2]:

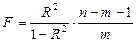, (12)

где R² – множественный коэффициент (индекс) детерминации.

Кроме этого способа, во множественной регрессии появляется еще один – F-критерий частный, определяющий целесообразность включения отдельного фактора после всех остальных. Используется следующая формула:

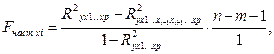(13)

где R²_x1…xp – индекс множественной детерминации для модели с полным набором факторов; R²_{x1…xi-1, xi+1…xp} – индекс множественной детерминации, но без включения в модель фактора х_i.

Фактическое значение частного F-критерия сравнивается с критическим (табличным) при 5% или 1%-ом уровне значимости и числе степеней свободы: k₁=1 и k₂=n-m-1. Если фактическое превышает критическое, то дополнительное включение фактора х_i в модель после факторов х₁, х₂..х_i-1, x_i+1…x_p статистически оправданно и коэффициент чистой регрессии b_i при факторе х_i статистически значим. Если наоборот, то дополнительное включение в модель фактора х_i после факторов х₁, х₂..х_i-1, x_i+1…x_p не увеличивает существенно долю объясненной вариации признака, следовательно, нецелесообразно его включение в модель.

Так как частный F-критерий косвенно оценивает значимость коэффициентов чистой регрессии, то существует взаимосвязь между ним и t-критерием для коэффициента регрессии при i-м факторе:

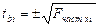(14)

Знак критерия зависит от знака коэффициента регрессии, для которого его определяют.

Присутствует оценка значимости отдельных коэффициентов множественной регрессии по t-критерию Стьюдента, позволяющая определять включение каждого фактора в модель. В этом случае, как и в парной регрессии, для каждого фактора используются формулы:

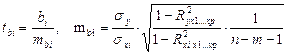, (15)

где s_y – среднее квадратическое отклонение для признака y; s_xi – среднее квадратическое отклонение для признака x_i; R²_yx1…xp – коэффициент детерминации для уравнения множественной регрессии; R²_{xi x1…xp} – коэффициент детерминации для зависимости фактора x_i со всеми другими факторами уравнения множественной регрессии.

Отбор факторов для уравнения осуществляется в две стадии: на первой подбираются факторы исходя из сущности проблемы; на второй – на основе матрицы показателей корреляции определяют t-статистики для параметров регрессии.

Коэффициенты корреляции между факторами (т. е. корреляции между объясняющими переменными) позволяют исключать из модели дублирующие факторы. Считается, что две переменные явно коллинеарны, т. е. находятся между собой в линейной зависимости, если r_х1х2³ 0, 7.

Поскольку одним из условий построения уравнения множе­ственной регрессии является независимость действия факторов, т.е. r_xixj=0, то коллинеарность факторов нарушает это условие. Ес­ли факторы явно коллинеарны, то они дублируют друг друга и один из них рекомендуется исключить из регрессии. Предпочте­ние при этом отдается не фактору, более тесно связанному с результатом, а тому фактору, который при достаточно тесной связи с результатом имеет наименьшую тесноту связи с другими факторами.

По величине парных коэффициентов корреляции обнаружи­вается лишь явная коллинеарность факторов. Наибольшие труд­ности в использовании аппарата множественной регрессии воз­никают при наличии мультиколлинеарности факторов, когда более чем два фактора связаны между собой линейной зависимос­тью, т.е. имеет место совокупное воздействие факторов друг на друга. Включение в модель мультиколлинеарных факторов нежела­тельно в силу следующих последствий:

• затрудняется интерпретация параметров множественной ре­грессии как характеристик действия факторов в «чистом» ви­де, ибо факторы коррелированны, параметры линейной рег­рессии теряют экономический смысл;

• оценки параметров ненадежны, колеблются с изменением объема наблюде­ний не только по величине, но и по знаку, что делает модель непригодной для анализа и прогнозирования; обнаруживаются большие стан­дартные ошибки.

Для оценки мультиколлинеарности факторов может быть использован определитель матрицы парных коэффициентов корреляции между факторами. Если бы факторы не коррелировали между собой, то матрица парных коэффициентов была бы единичной, т.к. все недиагональные элементы были бы равны 0, т.е. Det|R|=1. Если, наоборот, то все коэффициенты корреляции равны 1 и тогда определитель равен 0. Следовательно, чем ближе к 0 определитель матрицы, тем сильнее будет мультиколлинеарность факторов и ненадежнее результаты множественной регрессии.

Например, для 3 коррелируемых факторов определитель матрицы будет выглядеть следующем образом:

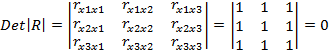(16)

Проверка мультиколлинеарности факторов может быть проведена методом испытания гипотезы о независимости переменных Н₀: Det|R|=1. Для этого находят фактическое значение критерия c² равное величине n-1-1/6*(2*m+5)*lgDet|R|. После чего сравнивают его с табличным, определенном при n*(n-1)/2 степенях свободы и уровне значимости a. Если фактическое превосходит табличное, то гипотеза Н₀ отклоняется.

Для характеристики относительной силы влияния х₁ и х₂ на у рассчитывают средние коэффициенты эластичности[6]:

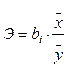(17)