
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Парная и множественная модель рентабельности собственного капитала
|
|
Рассмотрим влияние факторов на рентабельность собственного капитала при помощи парной и множественной модели, где у - рентабельность собственного капитала, %; х1- рентабельность продаж, тыс. руб.
Для расчета параметров уравнения линейной функции строим расчетную таблицу 5.
Таблица 5 - Данные и показатели для расчета параметров
| Года | x | y | x2 | y2 | y·x |
| 28, 51 | 14, 29 | 813, 02 | 204, 28 | 407, 54 | |
| 26, 98 | 11, 94 | 727, 99 | 142, 60 | 322, 19 | |
| 1, 93 | 0, 68 | 3, 74 | 0, 46 | 1, 31 | |
| 15, 73 | 7, 32 | 247, 45 | 53, 65 | 115, 22 | |
| 34, 88 | 12, 36 | 1216, 48 | 152, 78 | 431, 10 | |
| 3, 09 | 1, 11 | 9, 55 | 1, 23 | 3, 43 | |
| Сумма | 111, 13 | 47, 71 | 3018, 23 | 555, 00 | 1280, 80 |
| Среднее | 18, 52 | 7, 95 | 503, 04 | 92, 50 | 213, 47 |
Для расчета значений параметров нам понадобятся:
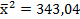 и
и 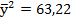 .
.
Линейная функция сводится к нахождению параметров уравнения вида:
yx = a + b 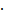 x (1)
x (1)
Уравнение данного вида позволяет по заданным фактическим значениям фактора x иметь теоретические значения результативного признака.
Для оценки параметров a и b используем систему (2) нормальных уравнений:
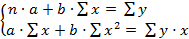 (2)
(2)
Подставим данные из таблицы 5, тогда система нормальных уравнений примет следующий вид:
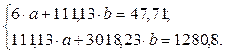
Решая систему нормальных уравнений либо методом последовательного исключения переменных, либо методом определителей найдем искомые оценки параметров a и b. Можно воспользоваться следующими готовыми формулами (3):
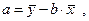
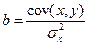
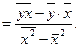
где 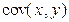 — ковариация признаков;
— ковариация признаков; 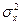 — дисперсия признака х.
— дисперсия признака х.
Подставим данные в формулы:
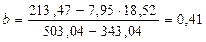
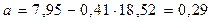
Используя полученные параметры a и b получим следующее уравнение регрессии:
yх = 0, 29 + 0, 41· x
Коэффициент регрессии b показывает, что при увеличении рентабельности продаж на 1%, рентабельность собственного капитала увеличится в среднем на 0, 41%.
Тесноту линейной связи оценим с помощью коэффициента корреляции. Для этого сначала найдем среднеквадратические отклонения х и у по формулам:
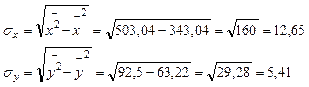
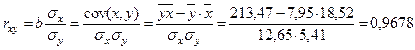
По шкале Чеддока можно сказать, что связь между рентабельностью продаж и рентабельностью собственного капитала является очень сильной.
Коэффициент детерминации равен:
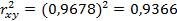
Мы получили, что 93, 66% вариации результативного признака (рентабельность собственного капитала, %) объясняется полученным уравнением регрессии, т.е. фактором рентабельность продаж, %. Только на 6, 34% оставшейся вариации уровня рентабельности собственного капитала приходятся прочие неучтенные в модели факторы.
Для расчета средней ошибки аппроксимации построим расчетную таблицу 6.
Таблица 6 - Вспомогательная таблица для расчета статистических величин
| Года | y | yx | │ y-yx│ | │ y-yx/y│ |
| 14, 29 | 11, 98 | 2, 31 | 0, 16 | |
| 11, 94 | 11, 35 | 0, 59 | 0, 05 | |
| 0, 68 | 1, 08 | 0, 40 | 0, 59 | |
| 7, 32 | 6, 74 | 0, 58 | 0, 08 | |
| 12, 36 | 14, 59 | 2, 23 | 0, 18 | |
| 1, 11 | 1, 56 | 0, 45 | 0, 40 | |
| Сумма | 47, 71 | 47, 30 | 6, 56 | 1, 46 |
| Среднее | 7, 95 | 7, 88 | 1, 09 | 0, 24 |
Определим качество модели через среднюю ошибку аппроксимации:

Качество модели можно оценить как плохое, т. к. `А превышает 8-10%.
Оценим значимость уравнения в целом с помощью F-критерия:
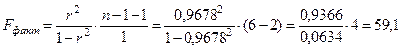
Определим критическое значения критерия по таблице при Fкр(m; n-m-1; a); Fкр(1; 4; 0, 05)=7, 71
Так как Fфакт > Fкр, то с вероятностью 95% можно утверждать, что уравнение регрессии является статистически значимым и гипотезу Н0 о случайном характере связи следует отклонить.
Оценку статистической значимости параметров регрессии проведем с помощью t-статистики Стьюдента, для этого определим стандартную ошибку для каждого параметра. Для того, чтобы рассчитать данные показатели, используем данные таблицы 7.
Таблица 7 – Вспомогательная таблица для расчета стандартных ошибок
| Годы | 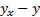
| 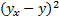
| 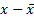
| 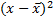
|
| -2, 31 | 5, 34 | 9, 99 | 99, 80 | |
| -0, 59 | 0, 35 | 8, 46 | 71, 57 | |
| 0, 40 | 0, 16 | -16, 59 | 275, 23 | |
| -0, 58 | 0, 34 | -2, 79 | 7, 78 | |
| 2, 23 | 4, 98 | 16, 36 | 267, 65 | |
| 0, 45 | 0, 20 | -15, 43 | 238, 1 | |
| ∑ | -0, 40 | 11, 36 | 0, 00 | 960, 12 |
Определим случайные ошибки mb, ma, mr:
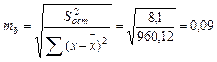
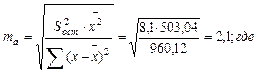
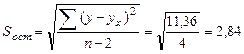
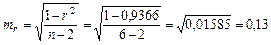
Тогда получим:
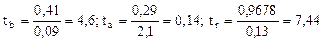
Найдем фактическое значение критерия tкр(n-m-1; a); tкр(4; 0, 05)=2, 78.
Так как tb> tкр, то с вероятностью 95% можно утверждать, что параметр b является статистически значимым и гипотезу H0 о равенстве его нулю следует отклонить.
Так как ta< tкр, то с вероятностью 95% можно утверждать, что параметр a статистически не значим и гипотезу H0 о равенстве его нулю следует принять.
Так как tr> tкр, то с вероятностью 95% можно утверждать, что коэффициент корреляции r статистически значим и гипотезу H0 о равенстве его нулю следует отклонить.
Найдем прогнозное значение рентабельности собственного капитала, подставив предполагаемое значение рентабельности продаж в уравнение регрессии при условии: xпр = 18, 52 · 1, 1 = 20, 37, тогда yпр = 0, 29+0, 41 · 20, 37 = 8, 64%.
Таким образом, прогнозный уровень рентабельности собственного капитала при предполагаемом значении рентабельности продаж составит 8, 64%.
Оценим качество прогноза, для этого рассчитаем ошибку прогноза и найдем доверительный интервал.
Найдем ошибку прогноза по следующей формуле:
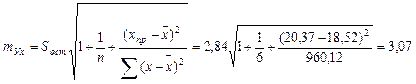
Доверительный интервал имеет вид:
yпр - tкрmУх £ ух пр £ упр + tкрmУх
Для того, чтобы рассчитать доверительный интервал, найдем значение
tкр(n-m-1; α), тогда tкр(6-1-1; 0, 05)=2, 78
8, 64 – 2, 78·3, 07 £ ух пр £ 8, 64+2, 78·3, 07
0, 11 £ ух пр £ 17, 17
Следовательно с вероятностью 95% можно утверждать, что уровень рентабельности собственного капитала (упр) находится в интервале от 0, 11 до 17, 17.
Рассмотрим множественную регрессию, когда в качестве второго фактора будет выступать собственный капитал, тогда получим:
у – рентабельность собственного капитала, %;
х1 – рентабельность продаж, %;
х2 – коэффициент оборачиваемости активов.
Логарифмическое уравнение множественной регрессии представляет собой следующий вид: у=a+b1x1+b2x2
Для нахождения его параметров решим систему из трех уравнений, воспользовавшись данными из таблицы 8.
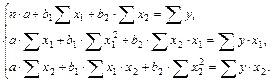
Таблица 8 – Исходные данные для расчета параметров
| № года | y | x1 | x2 | y·x1 | y·x2 | 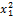
| 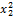
| 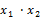
| 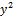
| |
| 16, 78 | 36, 64 | 0, 46 | 615, 00 | 7, 69 | 1342, 50 | 0, 21 | 16, 78 | 281, 73 | ||
| 14, 51 | 36, 08 | 0, 40 | 523, 56 | 5, 84 | 1301, 69 | 0, 16 | 14, 51 | 210, 58 | ||
| 12, 37 | 26, 48 | 0, 47 | 327, 46 | 5, 78 | 700, 95 | 0, 22 | 12, 37 | 152, 98 | ||
| 5, 64 | 15, 58 | 0, 36 | 87, 88 | 2, 04 | 242, 68 | 0, 13 | 5, 64 | 31, 82 | ||
| 7, 55 | 16, 95 | 0, 45 | 127, 92 | 3, 36 | 287, 39 | 0, 20 | 7, 55 | 56, 94 | ||
| 2, 01 | 4, 33 | 0, 46 | 8, 71 | 0, 93 | 18, 76 | 0, 22 | 2, 01 | 4, 05 | ||
| 14, 29 | 28, 51 | 0, 50 | 407, 54 | 7, 16 | 813, 02 | 0, 25 | 14, 29 | 204, 28 | ||
| 11, 94 | 26, 98 | 0, 44 | 322, 19 | 5, 29 | 727, 99 | 0, 20 | 11, 94 | 142, 60 | ||
| 0, 68 | 1, 93 | 0, 35 | 1, 31 | 0, 24 | 3, 74 | 0, 12 | 0, 68 | 0, 46 | ||
| 7, 32 | 15, 73 | 0, 47 | 115, 22 | 3, 41 | 247, 45 | 0, 22 | 7, 32 | 53, 65 | ||
| 12, 36 | 34, 88 | 0, 35 | 431, 10 | 4, 38 | 1216, 48 | 0, 13 | 12, 36 | 152, 78 | ||
| 1, 11 | 3, 09 | 0, 36 | 3, 43 | 0, 40 | 9, 55 | 0, 13 | 1, 11 | 1, 23 | ||
| Сумма | 106, 57 | 247, 18 | 5, 07 | 2971, 33 | 46, 52 | 6912, 20 | 2, 18 | 106, 57 | 1293, 11 | |
| Среднее | 8, 88 | 20, 60 | 0, 42 | 247, 61 | 3, 88 | 576, 02 | 0, 18 | 8, 88 | 107, 76 |
Система нормальных уравнений составит:
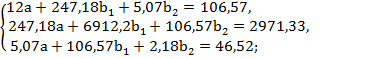
Решаем данную систему уравнений методом определителей: определитель системы 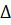 равен:
равен:
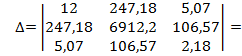 772, 92
772, 92
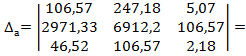 -4993, 05
-4993, 05
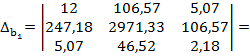 314, 93
314, 93
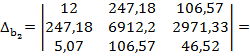 12710, 68
12710, 68
Найдем теперь сами параметры:
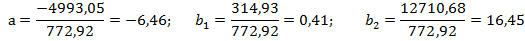
Получим уравнение регрессии: 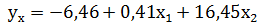
При увеличении рентабельности продаж на 1% уровень рентабельности собственного капитала увеличится в среднем на 0, 41% при неизменности коэффициента оборачиваемости активов.
При увеличении коэффициента оборачиваемости активов на единицу, рентабельность собственного капитала увеличится в среднем на 16, 45% при том же уровне рентабельности продаж.
На основе построенной модели спрогнозируем уровень результативного показателя на два года вперед при условии:
1 год: хпр1=1, 15*20, 6=23, 69 хпр2=1, 15*0, 42=0, 48
упр1=-6, 46+0, 41*23, 69+16, 45*0, 48=11, 15%
2 год: хпр1=1, 30*20, 6=26, 78 хпр2=1, 30*0, 42=0, 55
упр1=-6, 46+0, 41*26, 78+16, 45*0, 55=13, 57%
Таким образом, в первом прогнозируемом году рентабельность собственного капитала составит 11, 15%, если рентабельность продаж будет равна 23, 69%, а коэффициент оборачиваемости активов – 0, 48. Во втором прогнозируемом году рентабельность собственного капитала будет равна 13, 57%, если рентабельность продаж составит 26, 78%, а коэффициент оборачиваемости активов – 0, 55.
Найдем множественный коэффициент корреляции. Для этого рассчитаем парные коэффициенты корреляции:
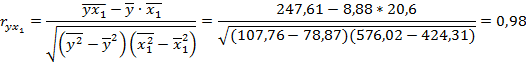
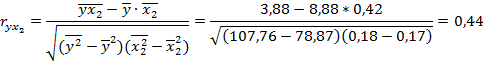
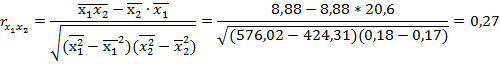
Следовательно, коэффициент множественной корреляции составит:
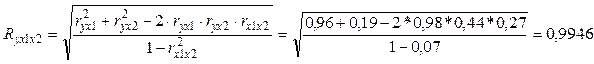
Показатель корреляции показывает на наличие очень сильной связи между факторами и результатом.
Значение коэффициентов парной корреляции указывают на сильную связь рентабельности собственного капитала с рентабельностью продаж – х1, и на умеренную связь с коэффициентом оборачиваемости активов – х2. Но в то же время rx1x2 =0, 27 указывает на отсутствие коллинеарности между факторами.
Скорректированный коэффициент корреляции рассчитаем по формуле:
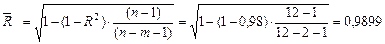
Скорректированный коэффициент корреляции немного уменьшил обычный показатель корреляции, сделав поправку на число степеней свободы.
Коэффициент детерминации равен 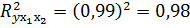
Зависимость у от х1 и х2 характеризуется сильной связью, в которой 98% вариации у определяется вариацией учтенных в модели факторов. Прочие факторы, не включенные в модель, составляют соответственно 2% от общей вариации у.
Рассчитаем частные коэффициенты корреляции первого порядка зависимости у от х1 и х2:
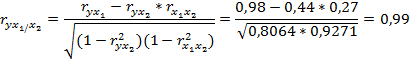
При закреплении фактора x2 на постоянном уровне корреляция у и х1 оказывается несколько выше (0, 99 против 0, 98).
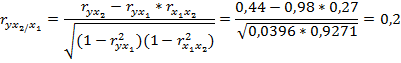
При закреплении фактора x1 на постоянном уровне корреляция у и х2 оказывается ниже (0, 2 против 0, 44).
Показатели частной корреляции не сильно отличаются от обычных парных коэффициентов корреляции – это связано с тем, что связь между факторами слабая неколлинеарная, поэтому в чистом виде степень тесноты связи у совпадает со значением коэффициентов парной корреляции.
Для характеристики относительной силы влияния х1 и х2 на у рассчитаем частные средние коэффициенты эластичности (26):
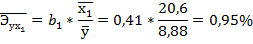
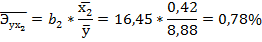
При увеличении рентабельности продаж на 1% от ее среднего уровня рентабельность собственного капитала возрастет на 0, 95% от своего среднего уровня, а рост коэффициента оборачиваемости активов на 1 увеличит рентабельность собственного капитала на 0, 78% от своего среднего уровня. Мы видим, что сила влияния рентабельности продаж – x1 на рентабельность собственного капитала оказалась несколько большей, чем сила влияния себестоимости – х2.
Значимость уравнения оценим через общий F- критерий Фишера:
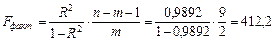
Табличное значение критерия при условии Fкр(m; n-m-1; α) будет равно
Fкр(2; 9; 0, 05)=4, 26.
Так как Fфакт> Fкр, то с вероятностью 95% можно утверждать, что уравнение является статистически значимым и гипотезу H0следует отклонить.
Для анализа существенности каждого фактора в модели используем частные F-критерии Фишера и оценку значимости каждого из параметров уравнения.
Найдем частные F-критерии Фишера по формулам:
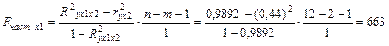
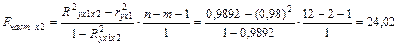
Табличное значение F-критерия при условии Fкр(1; n-m-1; α) будет ровняться Fкр(1; 9; 0, 05)=5, 12
Так как Fчаст х1> Fкр, то с вероятностью 95% можно утверждать, что фактор x1 является статистически значимым и его целесообразно включить после фактора x2.
Так как Fчаст х2> Fкр, то с вероятностью 95% можно утверждать, что фактор x2 является статистически значимым и его целесообразно включить после фактора x1.
Теперь проведем анализ с учетом значимости коэффициентов регрессии. Для этого вычислим t-критерии коэффициентов b1 и b2.
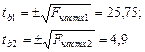
По таблице критических значений находим tкр(n-m-1; α)= tкр(9; 0, 05)=2, 26.
При сравнении фактических значений критерия Стьюдента с критическим получим, что коэффициенты b1 и b2 являются статистически значимыми. Это утверждение верно с вероятностью 95%. Поэтому фактор х2, силу которого оценивает b2, нельзя исключить как несущественно влияющий на результат.
Таким образом, обе проверки дали одинаковый результат. Общий вывод состоит в том, что множественная модель с факторами х1 и х2 не содержит неинформативных факторов. Построенная модель является хорошо детерминированной и пригодной для анализа и прогноза.
Так же данные показатели можно рассчитать автоматизировано с использованием пакета MS Excel. С помощью данной программы мы получили результаты корреляционно-регрессионного анализа (Приложение А), которые не сильно отличаются от рассчитанных в данном пункте, небольшие погрешности связаны с округлением.