
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Лекция 7. 3.4. Потенциальный барьер для скольжения дислокаций [сила Пайерлса]
|
|
3.4. Потенциальный барьер для скольжения дислокаций [сила Пайерлса]
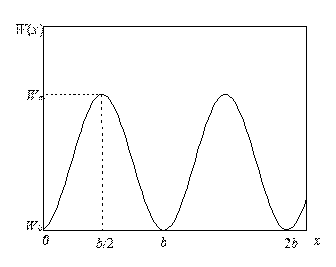
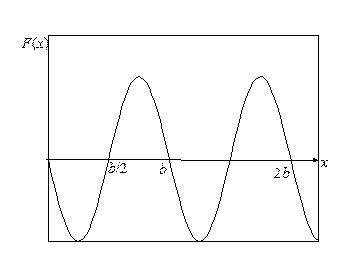
Зависимость энергии взаимодействия атомов W от смещения дислокации х при ее перемещении в плоскости скольжения (рис. 3.10) должна иметь вид периодической функции с периодом b (рис. 3.10). Производная dW (x) /dx в точке х= 0 должна обращаться в нуль. Действительно, производная dW (x) /dx есть сила, действующая на дислокацию F (x), и требование F (0) = 0 есть условие равновесия в исходном состоянии. Второе положение равновесия имеет место в точках F (b/ 2 +ib)(i – целое число). Взяв d 2 W (x) /dx 2, легко увидеть, что первое положение равновесия устойчивое, а второе неустойчивое. Зависимость F (x) приведена на рис. 3.11. Видно, что сила достигает максимума вблизи точки x ≈ b/ 4и по порядку величины (см. рис. 3.10 и 3.11) равна
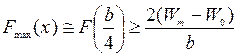 .
.
Более точные расчеты были проведены Френкелем и Конторовой, Пайерлсом и Набарро и др. Наиболее известна модель Пайерлса. Тело разбивается на два полупространства плоскостью скольжения (плоскость АА на рис. 3.7); считается, что к каждому из полупространств применима линейная теория упругости и что атомы, лежащие в плоскости скольжения, взаимодействуют с атомами противолежащего полупространства по периодическому закону, подобно изображенному на рис. 3.11. В качестве простейшего приближения был принят синусоидальный закон вида
 , [В. В.2] (3.10)
, [В. В.2] (3.10)
отличличающийся от (1.9) только введением двух постоянных решетки а и b вместо одной а.
| 
|
| Рис. 3.10. Возможный вид зависимости потенциальной энергии взаимодействия атомов от смещения дислокации х из начального положения равновесия | Рис. 3.11. Зависимость силы сопротивления решетки, действующей на дислокацию, от ее смещения из начального положения равновесия |
В этих приближениях величина W П = W – W 0 оказалась равной:
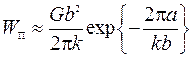 . (3.11)
. (3.11)
Критическое скалывающее напряжение σ П, необходимое для движения дислокации через рельеф W(x), равно (σ к ~ F max / b)
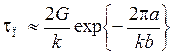 . (3.12)
. (3.12)
где, как и ранее, k = l для винтовой и k = 1 – v для краевой дислокации. Напряжение τ П часто называют напряжением Пайерлса.
Замечания к формулам (3.11) и (3.12):
1. Поскольку при выводе формул делались очень грубые предположения, они могут быть справедливы только качественно, количественные оценки могут совпадать с экспериментом только по порядку величины.
2. Напряжение τ П гораздо меньше теоретического напряжения для сдвига в идеальной решетке τ 0 ≈ G /6 [см. формулу (1.9)]. Так, для простой кубической решетки a=b, ξ = l/3 и k = 2/3 (краевая дислокация), τ п = 2, 5ּ 10 –4 G < < τ 0.
3. В (3.10) не учтены типы межатомных связей и типы кристаллических решеток. Величины W П и τ П для некоторых материалов с различными типами связей в решетке для плоскостей с максимальными значениями а/b даны в табл. 3.1.
4. Наиболее важный качественный вывод из формулы (3.11): τ П тем меньше, чем меньше вектор Бюргерса дислокации b, и тем больше, чем меньше расстояние а между плоскостями в нормальном к плоскости скольжения направлении. Даже при небольшом уменьшении a/b напряжение τ П меняется очень сильно. Например, для случая п.2 при a/b =1 τ П ≈ 2, 5ּ 10–4 G и при а/b =1, 5 τ П≈ 6ּ 10 –3 G, т. е. увеличивается примерно в 20÷ 25 раз. Поэтому большой подвижностью обладают только дислокации с маленькими векторами Бюргерса, лежащие в плоскостях, расстояние а между которыми велико. Легко сообразить, что двум этим требованиям, например, в ГЦК решетке удовлетворяют плотноупакованные плоскости типа {111}. Будем их называть плоскостями легкого скольжения.
Т а б л и ц а 3.1