
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Приближение линейного натяжения (определение прогиба дислокации)
|
|
Для оценки энергии дислокации часто пользуются формулой (3.19), т. е. считают энергию дислокации пропорциональной ее длине и не зависящей от ее формы. В этом приближении можно считать дислокацию трубкой в кристалле, обладающей избыточной энергией
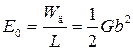 (3.27)
(3.27)
на единицу длины.
Известно, что коэффициент поверхностного натяжения жидкости можно рассматривать двояко: как силу, действующую на единицу длины мысленного разреза поверхности жидкости, или как избыточную энергию единицы поверхности. По аналогии с жидкостью энергию единицы длины дислокации w 0 одновременно можно рассматривать как силу, действующую перпендикулярно нормальному сечению дислокационной трубки, т. е. как силу, действующую вдоль касательной к линии дислокации. Поэтому дислокационную трубку можно представить как натянутый резиновый шнур с постоянной по длине силой натяжения Е 0. Такое представление дислокации и носит название «приближение линейного натяжения». Оно обычно используется для нахождения формы дислокационных отрезков в поле напряжений. Соответствующие задачи аналогичны задачам о форме натянутого резинового шнура, на который действуют распределенные силы.
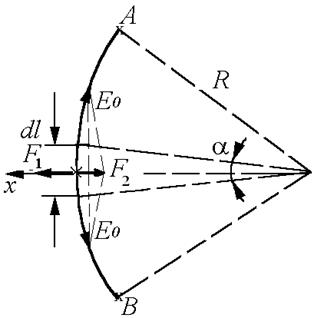
Рис. 3.18. Схема к задаче о нахождении равновесной конфигурации дислокационного отрезка, закрепленного на концах А и В, в поле постоянного напряжения τ
Рассмотрим, например, задачу о равновесии дислокационного отрезка, закрепленного на концах (рис. 3.18), в поле постоянного напряжения τ. На отрезок dl дислокации (при малом прогибе этот отрезок любой) вдоль оси х действуют силы
 .
.
Так как
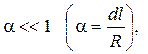 то F 1 +F 2=0,
то F 1 +F 2=0,
откуда
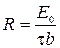 . (3.28)
. (3.28)
Таким образом, дислокационный отрезок равномерно прогнут с радиусом кривизны, определяемым формулой (3.28).
Считается, что приближение линейного натяжения применимо, если логарифмический член в формуле для энергии изменяется слабо. Для одиночных дислокаций приближение линейного натяжения может быть использовано для малых их прогибов, когда радиус их кривизны остается много больше их длины.