
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Скопление дислокаций
|
|
Энергия дислокаций в скоплении W ск на единицу длины может быть оценена следующим образом: на расстояниях от скопления r, больших его размера L, скопление ведет себя как супердислокация с вектором Бюргерса
B = n b,
где п – число дислокаций в скоплении. (Изменение длины отрезка, занимаемого дислокациями от L до nb, не должно быть существенным.) При r< < d (d – расстояние между соседними дислокациями) существенны напряжения только одной дислокации, при d< r< L простая оценка невозможна. Но из сказанного ясно, что формула для W ск должна иметь вид
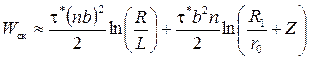 , (3.24)
, (3.24)
где R - радиус действия напряжений от скопления как супердислокации; d< R 1 < L –какой-то радиус «экранирования» для полей напряжений отдельных дислокаций. Первый член – энергия скопления вдали от него, второй - внутри скопления от отдельных дислокаций (их n штук.).
Первый член в этой формуле пропорционален n 2, второй – п. Следовательно, при достаточно больших n (практически при n> 7 ÷ 10) первый член будет больше второго, т. е. энергия скопления дислокаций с n > 10 много больше, чем энергия отдельных дислокаций, его составляющих. Поскольку всякая система стремится перейти в состояние с наименьшей энергией, то, следовательно, скопление дислокаций является неустойчивой конфигурацией и стремится к распаду на отдельные дислокации.
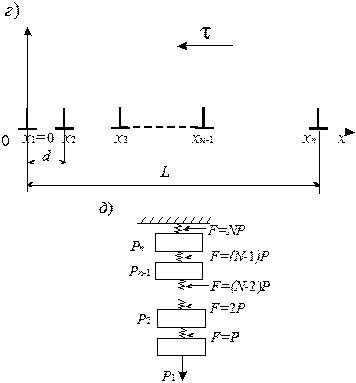
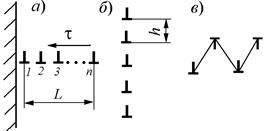 Рис. 3.17. Дислокационные конфигурации: а – скопление, поджатое напряжением τ к препятствию – неустойчивая конфигурация; б – стенка – устойчивая конфигурация; в – устойчивая конфигурация из двух скоплений противоположного знака; г - схема для расчета геометрии скопления; д - система последовательно подвешенных грузов - механический аналог скопления
Рис. 3.17. Дислокационные конфигурации: а – скопление, поджатое напряжением τ к препятствию – неустойчивая конфигурация; б – стенка – устойчивая конфигурация; в – устойчивая конфигурация из двух скоплений противоположного знака; г - схема для расчета геометрии скопления; д - система последовательно подвешенных грузов - механический аналог скопления
| 
|