
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
В) Расчет прочности.
|
|
А) Данный вид деформации возникает при нагружении ломаных стержней или валов редукторов.
В данном виде деформации в поперечном сечении изгибающие и крутящие моменты, которые продолжаются соответственно нормальными и касательными напряжениями.
При расчете прочности нельзя воспользоваться принципом суперпозиции, т.к. действующие напряжения разнородны(т.е. нормальные и кас-ые)
Нормальное напряжение от изгиба опр: 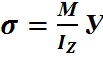
Кас-ое напряжение: 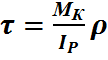 ;
; 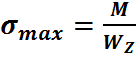 ;
; 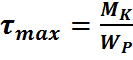
В данном случае для реализации условий прочности пользуются данными эквивалентного напряжения в результате учета нормального и касательного напряжений.
Эквивалентные напряжения получают на основании выводов теории прочности.
В настоящее время рассмотренный вид деформации наиболее достоверно описывается 3 и 4-ой теориями прочности. Эти теории определяют условие прочности следующими выражениями:
III 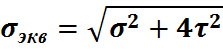 (1)
(1)
IV 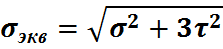 (2)
(2)
В) И 3-я и 4-я теории прочности считаются равноценными.
Определяемые по выр. (1) или (2) эквивалентные напряжения в опасном сечении учитываются в условии прочности
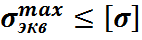 (3)
(3)
Условие прочности (3) записывается для опасных точек опасного сечения, которое выбирается след. образом:
1. сечение, где 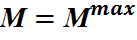 и
и 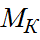 для этого сечения
для этого сечения
2. сечение 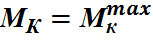 и соответствующее ему М
и соответствующее ему М
Замечание: после выполнения условия прочности для сечения 1 и 2 необходимо проверить ряд других сечений, в которых ни изгибающий, ни крутящий моменты не являются экстремальными.
Для круглого сплошного сечения осевой момент 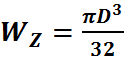 ;
; 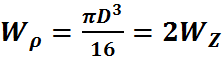 - полярный момент инерции
- полярный момент инерции
III 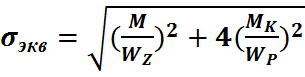 =
= 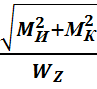 (*)
(*)
IV 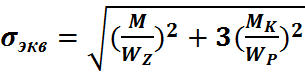 =
= 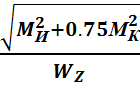 (*)
(*)
Подставляя (*) в (1) и (2), а затем используя это в (3) можно выполнять не только проверочный, но и проектный расчет, определяя размеры круглого сплошного сечения.
Замечание: в выражениях для нормальных напряжений рассматривается изгибающий момент, который может быть суммарным от изгиба в двух плоскостях, тогда он опред-ся:
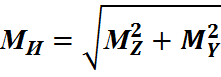
Б) При расчете прочности элементов конструкции в точках, которых возникает сложное напряженное состояние необходимо учитывать влияние различных компонентов расчета. Этот учет осуществляется введение теорий(гипотез)прочности.
Различные теории прочности основаны на определениях, предоставленных по причине характера разрушения.
Как правило, каждая из теорий прочности основывается на одном из критериев, например, считается, что разрушение происходит: 1.путем отрыва 2.путем скольжения частиц материала при деформации.
Следует заметить, что различные теории прочности имеют право на применение в случае экспериментального подтверждения.
Опасным состоянием элементов конструкции называется такое, при котором хотя бы в одной точке критерий прочности достигает предельного значения.
Рассмотрим некоторый элемент, в котором возникает напряженное состояние, характеризующееся главными напряжениями.
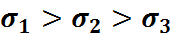
Первая теория прочности основана на представлении об отрыве частиц друг от друга. Считается, что условие выполнено если 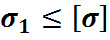 (4). Т.о. эта теория не учитывает напряжения
(4). Т.о. эта теория не учитывает напряжения 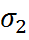 и
и 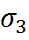 . Эта теория хорошо согласуется с экспериментом, когда
. Эта теория хорошо согласуется с экспериментом, когда 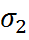 и
и 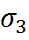
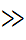
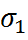 . В настоящее время эта теория не применяется.
. В настоящее время эта теория не применяется.
Вторая теория прочности
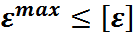 ;
; 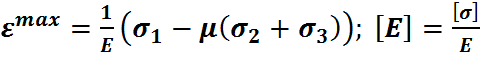 ;
;
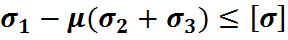 (5)
(5)
Третья теория прочности(наибольших касательных напряжений)
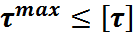 ;
; 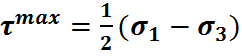 ;
; 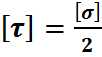 ;
;
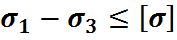 (6)
(6)
Недостатком этой теории явл. не учет промежуточного значения
Четвертая теория прочности

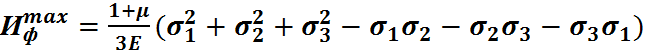
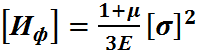
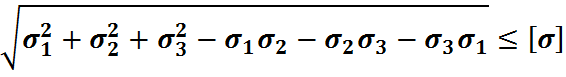 (7)
(7)
3-я и 4-я теории прочности наиболее хорошо согласуются с экспериментальными данными. Отклонения теоретических расчетов от экспериментальных не превышает 15%
В выр. (4)-(7) 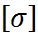 допускаемое напряжение для пластичного материала.
допускаемое напряжение для пластичного материала.
Для хрупкого материала попытки создать теорию прочности, еще более осложнены. Одна из таких теорий теория мощности Мора.
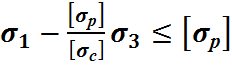 (8)
(8)
Выр.(8) учитывает хар-р материала и главные напряжения 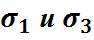
Представленные теории прочности испытывают для традиционных материалов, подчиняющихся гипотезам сложности, однородности, анизотропии. Не применимы для композитов.
5.Расчёт прочности при растяжении с изгибом.
Данный вид сопр. характерен для стержней- рам. Поперечные рамы являются основными стержневыми конструкциями каркасных зданий.
При нагружении в стержнях рам возникают изгибающие моменты поперечных и продольных сил.
Как правило, рамы наход. в состоянии прямого поперечного изгиба, поэтому изгибающий момент действует в плоскости рамы.
Расчет прочности по нормальным напряжениям в этом случае проводится следующим образом.
Нормальные напряжения опред.на основании принципа суперпозиции.
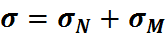
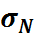 – доля напряж.от продольной силы.
– доля напряж.от продольной силы.
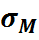 – доля напряж.от изгибающего момента.
– доля напряж.от изгибающего момента.
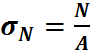

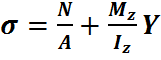
Это выражение определяет нормальное напряжение в точках с корд. y поперечного сечения, в котором действует продольная сила N и изгибающий момент Mz.

Условие прочности при растяжении с изгибом.
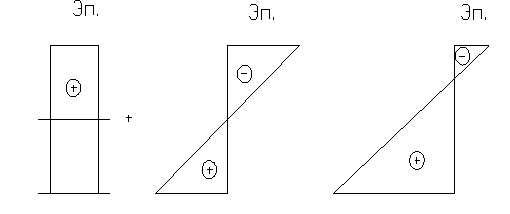
Опасные точки при данном виде сопротивления это точки наибольше удаленные от нейтральной оси при изгибе. Тогда maх напряжения опред.:
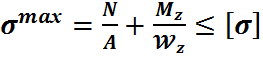
Это выражение необходимо реализовать для опасного сечения которое выбирается из следующего соображения:
1 ) 
2) 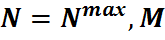
Проверку выполним по выражению 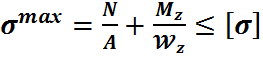 проектный расчет, поэтому же выражению.
проектный расчет, поэтому же выражению.
После выполнения проектного расчета для опасных сечений 1 и 2 необходимо проверить еще несколько сечений.