
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
А) Критическая сила. Формула Эйлера.
|
|
При рассмотрении сжатых стержней с ростом нагрузки растут и напряжения, определяемые выражением центра сжатия. Форма стержня остается прямолинейной. При достижении нагрузки некоторой величины наступает явление потери устойчивости прямолинейной формы равновесия. Наряду с прямолинейной формой существует и криволинейная. Сила, с которой наступает это явление, называется критической.
Изогнутая форма стержня описывается приближенным дифференциальным уравнением изогнутой оси.
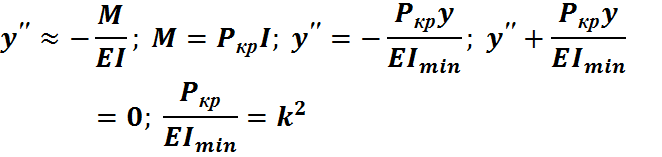
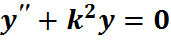
Уравнение однородное дифференциальное неполное уравнение второго порядка. Решение этого уравнения отыскивается в виде y=Asinkx+Bcoskx.
В этом выражении А и В произвольные постоянные. Постоянные А и В определяются из граничного условия(закреплены).
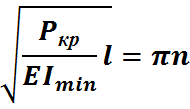
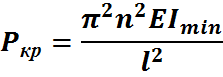
Выражение определяет семейство критических сил. Называем критической силой наименьшую силу, при которой происходит потеря таким образом выбирая величину 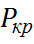 при n=1.
при n=1.
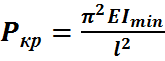 - формула Эйлера
- формула Эйлера
Как следует из выражения величина критической силы зависит от материала стержня и его геометрии.
Универсальная формула для критической силы должна быть записана в следуещем виде: 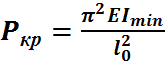
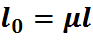 –приведенная длина стержня.
–приведенная длина стержня. 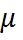 определяется условием опорных закреплений
определяется условием опорных закреплений