
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Основные классы булевых функций.
|
|
{, &, V, ~, →, ∆, /, ↓ }
{ ∆, /, ↓ } – добавочные.
1 класс. Р0 - класс булевых функций сохраняющие const 0.
это означает, что f(x1, ..., xn) при xi=0, 1≤ i≤ n, то f(0...0) должно быть равно 0.
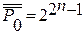 – мощность. Р0 = {f │ f (0, …, 0) = 0}
– мощность. Р0 = {f │ f (0, …, 0) = 0}
Р1 - класс булевых функций сохраняет const 1.
это означает, что f(x1,..., xn) при xi=1 равно 1.
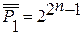 – мощность. Р1 = {f │ f (1, …, 1) = 1}
– мощность. Р1 = {f │ f (1, …, 1) = 1}
2 класс. S - класс самодвойственных булевых функций.
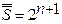
Функция f* называется двойственной по отношению к f(x1,..., xn), если имеет место следующее равенство 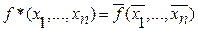
Функция является само двойственной, если 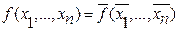
Функция является само двойственной, если при взятии отрицания всех переменных и плюс ко всему отрицание самой функции мы получим исходную функцию. 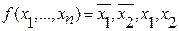
3 класс L - класс линейных функций.
Функция f(x1,..., xn) является линейной, если она представлена в виде полинома.
полином Жегалкина:
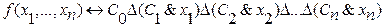
где Ci = const.
Пример линейной функции.
f(x1, x2)=x1∆ x2.
4 класс. М – монотонные функции.
Возьмем 2 набора (кортежа) одной размерности
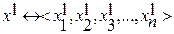
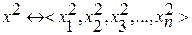
Набор x1 не меньше набора x2, если для всех xi выполняется 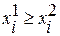
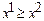 , если
, если 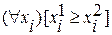

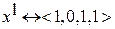 где 1=1, 0=0, 1=1, 1> 0 =>
где 1=1, 0=0, 1=1, 1> 0 => 
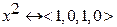
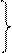 Если
Если 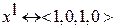 => наборы не сравнимые.
=> наборы не сравнимые.
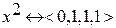
Функция f является монотонной, если в рассмотренных наборах имеется такое условие: 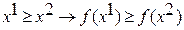
5 класс симметричных функций S
функция f(x1,..., xn) является симметричной если она сохраняет свое значение при любой перестановке аргумента.
f(x1,..., xn)↔ f(y1,..., yn)
где y1,..., yn – любая перестановка переменных.
Если взять функции одного(из данного) класса и применить к ним операции подстановки и суперпозиции, то получатся функции только данного класса.
Критерий Поста-Яблонского.
(критерий полноты системы булевых функций).
Для того, чтобы {f1,..., fm} – система функций была полной, необходимо и достаточно, чтобы она содержала хотя бы 1 функцию:
- Не сохраняющую нуль (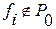 )
)
- Не сохраняющую единицу (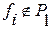 )
)
- Не являющуюся самодвойственной (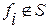 )
)
- Не являющуюся линейной (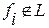 )
)
- Не являющуюся монотонной (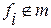 )
)
Примеры полных систем:
1) {, &, V }
2) {, & }
3) { / }
4) { ↓ }
5) { ∆, &, const f(0) }