Эйлеровы графы.

Мы говорим, что граф есть множество вершин, соедененных различными ребрами.

Граф является плоским, если любые пересечения ребер есть вершина, в противном случае, граф называется пространственный или объемный

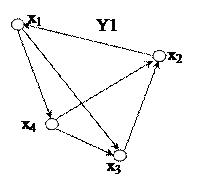Нас будет интересовать задача о нахождении наикратчайшего пути между вершинами графа. Путь между двумя вершинами проходит по ребрам.

Длиной маршрута называют количество ребер, участвующих в пути.

Длина маршрута х₂х₁х₄х₃х₂х₄ равен 5

Здесь встречаются циклы, например х₂х₃х₄х₂, в результате маршрут зацикливается, поэтому необходимо:

При задании маршрута желательно выделить циклы.

Можно ли пройти весь город пройдя по всем мостам лишь один раз. В вершине А сходится нечетное число ребер и заметили во всех вершинах это число четное.

Получили граф локальная степень вершин которого, не четная.Эйлер решил эту задачу отрицанием.

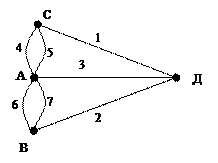Обобщением этой задачи послужила следующая постановка: можно ли указать такой граф обходя ребра которого точно 1 раз мы получим полный цикл на данном графе. В связи с постановкой задачи цикл называется Эйлеровым, т.е. маршрут проходят точно один раз по всем ребрам (повторение вершин допускается).

Если имеется не цикл, а цепь разорваный цикл, то соответсвующая цепь называется Эйлеровой, т.е. цепь маршрута, проходит по каждому ребру точно один раз. Ответом на эту задачу служит следующее утверждение: для того чтобы граф содержал Эйлерову цепь от вершины А к вершине В необходимо и достаточно, чтобы вершина А и В были единственными нечетными вершинами графа, при этом Элеровый граф, граф содержащий Эйлеровы цепи является связным.

На каком-то графе в общем случае неориентированном мы желаем выделить такое количество путей (цепей), чтобы с одной стороны стороны они были Эйлеровыми, а с другой стороны их количество было минимальным.

Имеет место следующие утверждение: На графе с (2R) вершинами можно выделить k Эйлеровых цепей.

Допустим, необходимо посетить выставку, обойдя все залы, и посещать всего 1 раз каждый из них

Задача о лабиринтах:

придя из точки А в точку A₁ мы помечаем поля направления, из точки А, выходят несколько ребер, необходимо пометить маршрут. Допустим отметили маршрут по часовой стрелке. Сюда относятся задачи о лабиринтах, выстовачных залах. Примерами являются задачи типа о волке, козе и капусте.

Задача о прохождении через ребра пройдя через каждую вершину только один раз. Эту задачу поставил Гамильтон в виде шутки: построить додекаэдр.

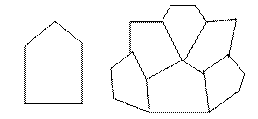должно получиться 12 граней.

Это задача – шутка рассмотрим следующим образом указать маршрут движения по ребрам додекаэдра единственный раз проходя через вершины.

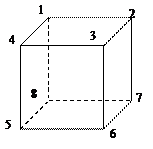
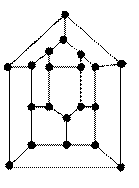Простейший пример: гамельтонова маршрута обход кубика, при этом мы обхватываем все вершины, но не все ребра.

Для того, чтобы получить гамильтонов цикл, нужно лишь замкнуть ребром 1-8

Путь (1524361) мы единственным образом попадаем во все вершины.
Эти задачи Гамильтон назвал задачами о комивояжоре (торговце): он обходит n городов его задача обойти все города, входя в них хотя бы по одному разу и пройти по кратчайшему пути.

Сюда относится задачи о линиях электропередач.

В 1971 годы была решена транспортная задача для города Ижевска. В городе имеется специальный автопарк, который обслуживает все торговые точки города. Необходимо было построить топографическую карту (схему улиц города).

Список литературы по разделу I

Элементы теории множеств.