Свойства дисперсии

Дисперсия обладает рядом свойств, которые позво­ляют упростить ее вычисления:

1. дисперсия постоянной величины равна нулю;

2. если все варианты значений признака уменьшить на одно и то же число С, то дисперсия не изменится (это означает, что дисперсия не зависит от начала отсчета);

3. если все варианты значений признака уменьшить (увеличить) в к раз, то дисперсия уменьшится (увеличиться) в к² раз (это означает, что величина дисперсии зависит от масштаба измерения исследуемого признака);

4. Дисперсия алгебраической суммы независимых случайных величин равна сумме их дисперсий:

5. Свойство минимальности дисперсии: , т.е. для любого постоянного числа, не равного средней арифметической, справедливо равенство,

Дисперсия не дает представления об однородности совокупности, по ней трудно дать экономическую интерпретацию, так как она рассчитывается в квадратных единицах. Эту проблему можно преодолеть, рассчи­тав среднее квадратическое отклонение.

В ходе расчетов следует помнить, что размах вариации, среднее линейное и среднее квадратическое отклонение являются именованными величинами, т.е. имеют ту же единицу измерения, что и изучаемый признак. Дисперсия единицы измерения не имеет.

Среднее квадратическое отклонение является абсолютной ме­рой вариации и представляет собой корень квадратный из диспер­сии:

Смысловое содержание этого показателя такое же, как и сред­него линейного отклонения: чем меньше его величина, тем од­нороднее совокупность и тем, соответственно, типичнее средняя величина.

Формулы для расчета среднего квадратического отклонения имеют следующий вид:

• для несгруппированных данных (простое):

• для сгруппированных данных (взвешенное):

Величина часто используется в качестве единицы измерения отклонений от средней арифметической. Отклонение, выраженное в , называется нормированным (стандартизованным).

Среднее квадратическое отклонение по своей величине всегда превышает значение среднего линейного отклонения в соответствии со свойством мажорантности средних.

В симметричных распределениях среднее квадратическое отклонение составляет приблизительно 1, 25 среднего линейного отклонения, т.е. или

Это соотношение зависит от наличия в совокупности резких отклонений и может служить индикатором «засоренности» совокупности нетипичными, выделяющимися из основной массы единицами.

Дисперсия и среднее квадратическое отклонение являются наиболее широко применяемыми показателями вариации. Это объясняется тем, что они входят в большинство теорем теории вероятностей, служащих фундаментом математической статистики. Также дисперсия может быть разложена на составные элементы, позволяющие оценить влияние различных факторов на вариацию признака. В последующих главах будет показано, как дисперсия используется для построения показателей тесноты корреляционной связи, при оценке результатов выборочных наблюдений и т.д.

Квартильное отклонение ,

где: и - соответственно третий и первый квартиль распределения.

Оно применяется вместо размаха вариации, чтобы избежать недостатков, связанных с использованием крайних значений.

В симметричных или умерено асимметричных распределениях выполняется равенство: 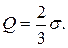Так как на квартальное отклонение не влияют отклонения всех значений признака, то его следует использовать, когда определение среднего квадратического отклонения затруднительно или невозможно. Например, этот показатель может применяться для рядов распределения с открытыми интервалами, где в качестве характеристики центра распределения использовалась медиана.

Дисперсия и среднее квадратическое отклонение используются в следующих случаях:

§ расчеты, связанные с организацией выборочного наблюдения;

§ оценка полученных на основе выборки статистических показателей;

§ построение показателей тесноты корреляционной связи.

В условиях нормального (симметричного) распределения существует следующая зависимость между величиной среднего квадратического отклонения и количеством наблюдений (правило «трех сигм»):

§ в пределах располагается 0, 683 количества наблюдений;

§ в пределах располагается 0, 954 количества наблюдений;

§ в пределах располагается 0, 997 количества наблюдений.

Отклонение ±3 можно считать максимально возможным.

Для оценки интенсивности вариации, а также для сравнения ее ве­личины в разных совокупностях или по разным признакам использу­ют относительные показатели вариации, которые рассчитываются как отношение абсолютных показателей вариации к средней величине признака (или медиане). К ним относятся:

§ Коэффициент осцилляции: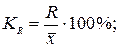

§ Относительно линейное отклонение:

§ Относительный показатель квартильной вариации:

§ Коэффициент вариации:

Наиболее часто применяется коэффициент вариации. Его применяют не только для сравнительной оценки вариации, но и для характеристики однородности совокупности.

Чем больше величина коэффициента ва­риации , тем больше разброс значений признака вокруг средней, тем больше неоднородность совокупности. Существует шкала определе­ния степени однородности совокупности в зависимости от значений коэффициента вариации (табл. 6.1).

Таблица 6.1