Показатели вариации

Для измерения вариации признака используются абсолютные и относительные показатели вариации.

Показатели вариации рассчитываются для статистических совокупностей, упорядоченных путем группировок, классификаций, построения рядов распределений.

Расчет показателей вариации позволяет:

1) дать характеристику отклонения отдельных значений признака от общей средней;

2) оценить однородность статистической совокупности.

Для характеристики размера вариации в статистике применяются абсолютные показатели вариации:

• размах вариации (R);

• среднее линейное отклонение ();

• дисперсия ;

• среднее квадратическое отклонение .

Размах вариации R (размах колебаний) - представляет собой разность между максимальным х_тax. и минимальным x_min. значениями при­знака:

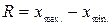
Размах вариации зависит от величины только крайних значений признака и не отражает его колеблемость внутри совокупности.

Для группировок с открытым интервалами (первым и последним), когда неизвестны реальные минимальные и максимальные значения признака, расчет размаха вариации некорректен.

Поэтому область его применения ограничена достаточно однородными совокупностями. В частности, на практике он находит применение в предупредительном контроле качества продукции.

Более точно характеризуют вариацию признака показатели, основанные на учете колеблемости всех значений признака. Среднее линейное отклонение и среднее квадратическое отклонение показывают, на сколько в среднем отличаются индивидуальные значения признака от его среднего значения. Эти показатели имеют те же единицы измерения, что и варианты признака, и его средняя величина. Порядок расчета показателей различен для несгруппированных и сгруппированных данных.

Среднее линейное отклонение () - это средняя арифметическая из абсолютных значений отклонений отдельных вариантов 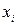признака от средней арифме­тической .

Для расчета этого показателя применяют сле­дующие формулы:

• для несгруппированных данных (простое):

где: 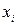- индивидуальные значения признака у единицы совокупности;

- сред­няя величина признака в совокупности;

n - число единиц совокуп­ности.

• для сгруппированных данных (взвешенное):

Простое среднее линейное отклонение вычисляется в случае, когда каждый вариант повторяется один раз, а расчет взвешенного среднего линейного отклонения производится на основе вариационного ряда с неравными частотами.

В расчетах по указанным формулам отклонения представлены без учета знака. Это объясняется тем, что по свойству средней арифметической сумма отклонений индиви­дуальных значений признака от средней равна нулю. Поэтому сфера применения среднего линейного отклонения как меры вариации признака ограничена, за исключением тех случаев, когда суммирование показа­телей без учета знаков имеет экономический смысл. В связи с этим более широкое распространение в качестве показателя степени ва­риации получило среднее квадратическое отклонение .

Дисперсия - это средний квадрат отклонений значе­ний признака от их средней величины.

В зависимости от исходных данных, дисперсию можно вычислять по средней арифметической простой или взве­шенной.

Для ее расчета используют следующие формулы:

• для несгруппированных данных (простая):

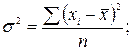
• для сгруппированных данных (взвешенная):

Формулу для расчета дисперсии можно преобразовать:

Таким образом, дисперсия равна разности средней из квадратов индивидуальных значений признака минус квадрат средней величины. Следовательно,

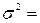
При использовании этой формулы исключается дополнительная процедура по расчету отклонений индивидуальных значений признака от его средней величины. В результате, за счет этого уменьшается ошибка, связанная с округлением значений промежуточных вычислений.