Малая выборка

В практике статистических исследований часто приходится сталкиваться с малыми выборками, которые имеют объем менее 30 единиц. К большим же обычно относят выборки объемом свыше 100 единиц.

Обычно малые выборки применяются в случаях, когда невозможно или нецелесообразно использовать большую выборку. Иметь дело с такими выборками приходится, например, при опросах туристов и посетителей гостиниц.

Величина ошибки малой выборки определяется по формулам, отличающимся от формул для сравнительно большого объема выборки ().

При малом объеме выборки n следует учитывать взаимосвязь между выборочной и генеральной дисперсией :

Так как при малой выборке дробь имеет существенное значение, то вычисление дисперсии производится с учетом, так называемого числа степеней свободы . Оно понимается как число вариантов 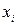, которые могут принимать произвольные значения, не меняя величины средней .

Средняя ошибка малой выборки определяется по формуле:

Предельная ошибка выборки для средней и доли находится аналогично случаю большой выборки:

где t – коэффициент доверия, зависящий от заданного уровня значимости и числа степеней свободы (Приложение 5).

Значения коэффициента зависят не только от заданной доверительной вероятности , но и от объема выборки n. Для отдельных значений t и n доверительная вероятность определяется по распределению Стьюдента, которое содержит распределения стандартизованных отклонений:

.

Замечание. По мере увеличения объема выбор­ки распределение Стьюдента приближается к нормальному распределению: при n =20 оно уже мало отличается от нормального распределе­ния. При проведении малых выборочных обследований следует учесть, что чем меньше объем выборки n, тем больше раз­личие между распределением Стьюдента и нормальным рас­пределением. Например, при п_min. = 4 это различие весьма существенно, что говорит об уменьшении точности результатов малой выборки.

Распределение Стьюдента применяется для решения следующих задач малой выборки:

1) оценка средней и доли по малой выборке;

2) интервальная оценка по малой выборке.