Ошибки выборки

Выборочное наблюдение носит несплошной характер, поэтому оно сопровождается ошибками (погрешностями).

Ошибки выборочного наблюдения возникают в двух случаях: 1. при сборе данных (ошибки регистрации); 2. в результате неполного учета единиц генеральной совокупности (ошибки репрезентативности).

Таким образом, любому выборочному наблюдению свойственна ошибка репрезентативности - расхождение между характеристиками выборочной и генеральной совокупности (рис 7.1).

Рис 7.1. Виды ошибок репрезентативности

Ошибка репрезентативности возникает в результате того, что вы­борочная совокупность не полностью отражает закономерности, присущие генеральной совокупности. Величина случайной ошибки репрезентативности зависит:

1) от объема выборки;

2) от степени вариации признака в генеральной совокупности;

3) от метода отбора единиц и т.д.

По данным выборочной совокупности оценивают показатели (параметры) генеральной совокупности. Например, используют оценку 2-х параметров:

- генеральной средней величины изучаемого признака (для количественного признака);

- генеральной доли (для альтернативного признака).

Теоретическое обоснование появления случайных ошибок выборки объясняют предельные теоремы теории вероятностей. Так как случайная ошибка выборки возникает в результате случайных различий между границами выборочной и генераль­ной совокупностей, то при достаточно большом объеме выборки эта ошибка будет сколь угодно мала. Поэтому характеристики выборки могут достаточно хорошо представлять характеристики генеральной совокуп­ности. Случайные ошибки могут быть доведены до незначительных размеров, что позволит определить их размеры и пределы с достаточной степенью точности на основании закона больших чисел.

Выборочное распределение средней величины будет прибли­жаться к нормальному распределению по мере увеличения объема выборки 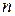, незави­симо от характера распределения генеральной совокупности. С увеличением численности выборки 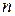величина выборочной средней приближается к генеральной средней .

Одной из задач выборочного метода является определение ошибок выборки, т.е. возможных расхождений характеристик совокупностей:

1) между выборочной средней ()и генеральной средней ();

2) между выборочной долей еди­ниц , обладающих изучаемым признаком, и генеральной до­лей (р).

Методы математиче­ской статистики позволяют измерить эти ошибки и указать границы их колеблемости. Величину ошибок можно оценить по формулам:

; .

В статистике различают три вида ошибок выборки:

- средняя ошибка ;

- предельная ошибка ;

- относительная ошибка .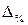

Вид формулы средней ошибки выборки зависит от метода отбора. Рассмотрим порядок расчета ошибок выборки при собственно-случайном отборе.

Средняя ошибка выборки - характеризует среднюю величи­ну возможных расхождений выборочных (средняя , доля ) и генеральных характеристик (средняя , доля ) совокупности. Представляет собой среднее квадратическое отклонение возможных значений характеристик выборочной совокупности от характеристик генеральной совокупности.

Рассмотрим формулы средней ошибки выборки длясредней и доли при повторном и бесповторном отборе:

1. При повторном отборе:

1.1. Средняя ошибка выборочной средней :

1.2. Средняя ошибка выборочной доли :

2. При бесповторном отборе:

2.1. Средняя ошибка выборочной средней :

2.2. Средняя ошибка выборочной доли :

где - дисперсия признака в генеральной совокупности;

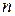- объем выборки;

- выборочная доля единиц, обладающих изучаемым признаком; дисперсия доли (альтернативного признака).

Замечание. На практике величина дисперсии признака в генеральной совокупности , как правило, неизвестна. Поэтому в формулы ошибки выборки подставляют дисперсию выборочной совокупности . Это возможно, поскольку между дисперсиями генеральной и выборочной совокупностей существует следующая взаимосвязь:

При большой численности выборочной совокупности 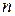сомножитель стремится к единице, и выборочная дисперсия практически совпадает с генеральной , т.е. .

Замечание. Поскольку при бесповторном отборе в ходе выборки объем генеральной совокупности сокращается, то в формулу для расчета средней ошибки включают дополнительный множитель .

Средняя ошибка выборки при собственно-случайном повторном отборе зависит от:

- объема выборки 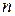(обратная зависимость);

- степени вариации признака (прямая зависимость).

Чем больше вариация признака, тем больше ошибка выборки. Для ее уменьшения необходимо увеличить объем выборочной совокупности.

Формулы расчета средних ошибок для различных методов отбора приведены в табл. 7.2.

Таблица 7.2

Формулы средних ошибок для различных методов отбора

Метод отбора	Оцениваемый параметр	Вид отбора
повторный	бесповторный
Собственно-случайный и механический	средняя
доля
Типический (пропорциональный)	средняя
доля
Серийный	средняя
доля
Комбинированный:   - типический и серийный     - собственно-случайный и серийный	cредняя
cредняя

Условные обозначения в таблице:

- средняя из групповых дисперсий;

доля единиц i -й типической группы (серии) выборки, обладающих изучаемым признаком;

- средняя из групповых дисперсий для доли.

М, m – количество равных серий соответственно в генеральной и выборочной совокупностях;

- межгрупповая выборочная дисперсия,

где средняя в i -й серии; общая выборочная средняя;

- межгрупповая выборочная дисперсия доли, где - доля единиц, обладающих признаком в выборке. При равновеликих сериях

Следует иметь в виду, что в каждой конкретной выборке разность может быть меньше, больше или равна величине средней ошибки . Вероятность такой ошибки различна. Поэтому рассчитывают предельную ошибку выборки .

Предельная ошибка выборки - это максимально возможное расхождение характеристик выборочной (средняя , доля ) и генеральной совокупности (средняя , доля ), т.е. максимум ошибки при заданной вероятности ее появления.

Величина предельной ошибки определяется по формуле:

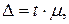
где - коэффициент доверия, который определяется по таблице значений интеграла Лапласа при заданной доверительной вероятности Он показывает, во сколько раз предельная ошибка выборки отличается от средней ошибки.

Соответственно, формулы предельной ошибки для средней и доли , имеют вид:

Значения интеграла Лапласа табулированы в зависимости от значений коэффициента (Приложение 2). Поэтому на практике пользуются готовыми таблицами значений. Приведем наиболее часто употребляемые уровни доверительной вероятности и соответствующие им значения :

	1, 0	1, 96	2, 0	2, 58	3, 0
	0, 683	0, 950	0, 954	0, 990	0, 997

Таким образом, предельная ошибка выборки отвечает на вопрос о точности выборки с определенной вероятностью, величина которой зависит от значения коэффициента доверия t.

Например, при t = 1 с вероятностью 0, 683 можно утверждать, что расхождение между выборочными и генеральными характеристиками не превысит одной величины средней ошибки выборки, т.е.

При t = 2 вероятность =0, 954, значит, в среднем 954 выборки из 1000 дадут показатели выборки (средняя , доля ), которые будут отличаться от генеральных показателей (средняя , доля ) не более чем на величину двукратной средней ошибки выборки, т.е. или

Появление ошибки в три раза большей, чем средняя ошибка выборки, маловероятно (1-0, 997=0, 003), и считается практически невозможным событием.

Пределы, в которых с данной вероятностью будет находиться неизвестная величина изучаемого показателя генеральной совокупности, называют доверительным интервалом, а вероятность - доверительной вероятностью.

В качестве доверительной вероятности обычно принимают значения вероятностей Р и соответствующие им уровни значимости (табл. 7.3)

Таблица 7.3

Соотношение между значениями доверительной вероятности

и уровнями значимости

Вероятность	Уровень значимости
0, 90	0, 10, или 10 %
0, 95	0, 05, или 5 %
0, 99	0, 01, или 1 %

Например, 10 %-ный уровень значимости означает, что в 90 случаях из 100 характеристика генеральной совокупности, выявленная на основе выборки, будет лежать в пределах доверительного интервала. То есть, в 10 случаях из 100 существует риск совершить ошибку по выборочным данным при оценке генеральной совокупности.

Очевидно, что чем больше значение предельной ошибки , тем больше величина доверительного интервала, т.е. ниже точность оценки.

Формулы предельной ошибки позволяют определить:

§ доверительные интервалы, в которых будут находиться значения генеральных параметров:

- генеральная средняя:

- генеральная доля:

§ необходимую численность выборки 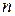, обеспечи­вающую с определенной вероятностью заданную точность наблюдения ();

§ вероятность допуска той или иной заданный ошибки (определяется и находится вероятность).

Наряду с абсолютной величиной предельной ошибки выборки рассчитывают и относительную ошибку выборки . Она определяетсякак процентное отношение предельной ошибки выборки к соответствующей характеристике выборочной совокупности (средняя , доля ):

§ для средней =

§ для доли

Выборка считается репрезентативной, если 5 %.

Пример. В порядке случайной бесповторной выборки было обследовано n = 160 турфирм из N = 1500, и получены следующие данные об их объеме продаж за отчетный период (табл. 7.4).

Таблица 7.4