
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Асимметрия распределения
|
|
Как уже отмечалось в § 5.3, если большая часть совокупности расположена левее центра распределения, имеет место левосторонняя асимметрия ( < Ме < Мо), а если правее – правосторонняя (Мо < Ме <
< Ме < Мо), а если правее – правосторонняя (Мо < Ме <  ).
).
Простейшей мерой асимметричности распределения является отклонение между характеристиками центра распределения. Поскольку в симметричном распределении 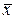 = Me = Мо, то чем заметнее асимметрия, тем больше отклонение (
= Me = Мо, то чем заметнее асимметрия, тем больше отклонение (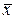 -Мо).
-Мо).
Для сравнительного анализа степени асимметрии нескольких распределений рассчитывается коэффициент асимметрии Пирсона:

Если значение  < 0, то асимметрия является левосторонней (скошенность влево). При
< 0, то асимметрия является левосторонней (скошенность влево). При  =0 распределение является симметричным (
=0 распределение является симметричным (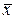 = Me = Мо). Если
= Me = Мо). Если  > 0, то наблюдается правосторонняя асимметрия (скошенность вправо). При этом для правосторонней асимметрии выполняется неравенство
> 0, то наблюдается правосторонняя асимметрия (скошенность вправо). При этом для правосторонней асимметрии выполняется неравенство  > Me > Mo, а длялевосторонней -
> Me > Mo, а длялевосторонней -  < Me < Mo.
< Me < Mo.
Чем больше абсолютная величина коэффициента, тем больше степень асимметрии. Принято считать, что если  , то асимметрия незначительна. Если
, то асимметрия незначительна. Если  , то асимметрия значительная.
, то асимметрия значительная.
Графическое изображение асимметрии распределения представлено на рис. 6.3.


Рис. 6.3. Асимметрия распределения
Для выявления асимметрии используют несколько показателей. Наиболее надежным считается нормированный коэффициент асимметрии третьего порядка, основанный на вычислении момента третьего порядка:

где:  - центральный момент третьего порядка.
- центральный момент третьего порядка.
Он не зависит от масштаба, выбранного при измерении варианта, так как является отвлеченной величиной.
Чтобы можно было сравнивать асимметричность в разных рядах,  сопоставляют со средним квадратическим отклонением в кубе.
сопоставляют со средним квадратическим отклонением в кубе.
На направление асимметрии указывает знак коэффициента:
§  < 0 - в ряду распределения преобладают варианты, которые меньше, чем средняя, т.е. ряд отрицательно асимметричен (левосторонняя скошенность - более длинная ветвь влево);
< 0 - в ряду распределения преобладают варианты, которые меньше, чем средняя, т.е. ряд отрицательно асимметричен (левосторонняя скошенность - более длинная ветвь влево);
§  > 0 - для ряда распределения характерна положительная асимметрия (правосторонняя скошенность - более длинная ветвь вправо);
> 0 - для ряда распределения характерна положительная асимметрия (правосторонняя скошенность - более длинная ветвь вправо);
§  = 0 - симметричное распределение, так как варианты равноудалены от
= 0 - симметричное распределение, так как варианты равноудалены от  и имеют одинаковую частоту, поэтому
и имеют одинаковую частоту, поэтому  = 0.
= 0.
Оценка степени существенности асимметрии дается с помощью средней квадратической ошибки  , которая зависит от объема наблюдений n и рассчитывается по формуле:
, которая зависит от объема наблюдений n и рассчитывается по формуле:
 =
= 
Если 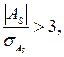 то асимметрия существенна и распределение признака в совокупности не является симметричным.
то асимметрия существенна и распределение признака в совокупности не является симметричным.
Если  то асимметрия несущественна, ее наличие объясняется влиянием случайных факторов.
то асимметрия несущественна, ее наличие объясняется влиянием случайных факторов.