Эксцесс распределения

Для симметричных распределений рассчитывается показатель эксцесса (островершинности). Термин «эксцесс» происходит от лат. «excssus» - отступление, излишество.

Эксцесс – это островершинность или плосковершинность распределения по сравнению с симметричным распределением при той же силе вариации.

Другими словами, эксцесс представляет собой отклонение вершины эмпирического распределения вниз или вверх от вершины кривой симметричного (нормального) распределения. При этом эксцесс определяется только для симметричных и умерено асимметричных распределений.

Показатель эксцесса основан на использовании центрального момента четвертого порядка, и рассчитывается по формуле:

где 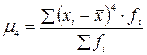- центральный момент четвертого порядка.

Знак коэффициента определяет вид распределения:

§ если 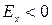- плосковершинное распределение;

§ если 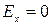- симметричное распределение;

§ если 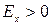- островершинное распределение.

На рис. 6.4 представлены различные виды распределений в зависимости от значений показателя эксцесса.

Рис. 6.4. Эксцесс распределений

Например, при отрицательной величине эксцесса распределение является плосковершинным по сравнению с нормальным распределением. Предельным значением отрицательного эксцесса является значение .

При положительной величине эксцесса, распределение более островершинное, чем нормальное. Величина положительного эксцесса является бесконечной.

В симметричном (нормальном) распределении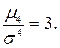

Средняя квадратическая ошибка эксцесса зависит от числа наблюдений n и рассчитывается по формуле:

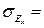
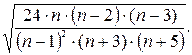
Если отношение принимает значение то отклонение от симметричного распределения считается существенным. Это свидетельствует о существенном характере эксцесса.

Оценка существенности показателей асимметрии и эксцесса позволяет сделать вывод о том, можно ли отнести данное эмпи­рическое распределение к типу нормального распределения.

Контрольные вопросы

1. Что понимают под вариацией признака и чем вызвана необходимость ее изучения?

2. Назовите абсолютные и относительные показатели вариации, дайте их характеристику.

3. Перечислите свойства дисперсии.

4. Сформулируйте «правило трех сигм».

5. В каком случае совокупность единиц считается неоднородной?

6. Как определяются средняя величина и дисперсия альтернативного признака?

7. В чем состоит правило сложения дисперсий?

8. С какой целью используются разные виды дисперсий?

9. Как оценивают тесноту связи между признаками?

10. Какие показатели структуры распределения вам известны?

11. Какие показатели формы распределения вам известны?

12. Дайте определение понятия моментов распределения. Какие моменты распределения вы знаете?

13. В чем состоит метод моментов?

14. Расскажите об асимметрии распределения и методах ее оценки.

15. Что называют эксцессом распределения?

16. С какой целью применяется оценка существенности показателей асимметрии и эксцесса?