Моменты распределения первых четырех порядков

Порядок момента к	Момент распределения
начальный	центральный	условный
Нулевой (к =0)
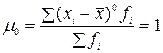
Первый (к =1)
Второй (к =2)
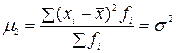
Третий (к =3)
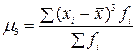
Четвертый (к =4)

Однако вычисления по данным формулам достаточно громоздки. Поэтому для их упрощения используют закономерности взаимосвязи между начальными, центральными и условными моментами:

;

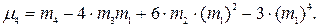
Анализ табл. 6.4 позволяет сделать следующие выводы:

§ начальный момент первого порядка представляет собой сред­нюю арифметическую ;

§ центральный момент первого порядка (нулевое свойство средней арифметической) всегда равен нулю;

§ центральный момент второго порядка – дисперсия ;

§ центральный момент третьего порядка используется при определении показателя асимметрии, для характеристики асимметричного распределения, ибо для симметричных рядов всегда ;

§ центральный момент четвертого порядка используется при определении показателя эксцесса.

Рассмотри подробно условные моменты . С их помощью упрощаются вычисления основных характеристик.

При к = 0 получаем начальный момент относительно нуле­вого порядка:

;

При к = 1 получаем момент первого порядка:

и т.д.

Из последней формулы следует, что = + , т.е. средняя арифметическая равна условному моменту первого порядка плюс начало отсчета .

Если отклонения () разделить на общий множитель , а затем умножить полученный момент на этот множитель в соответствующей степени, то, приходим к следующему равенству,

,

где – общий множитель.

Значит, = + .

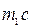Следует заметить, что вычисление средней методом отсчета от условного нуля называют методом моментов.

На практике начальные моменты относительно определяются следующим образом:

1. Из всех вариантов вычитают начало отсчета и находят отклоне­ния ;

2. Делят отклонения на общий множитель: ;

3. Вычисляют начальные моменты относительно х'.

4. Умножают найденные начальные моменты на .

Таким образом, в результате такого умножения получают искомые начальные моменты относительно .

Замечание. Метод моментов применяется при расчете средних величин в вариационных рядах с равными интервалами. Расчет ведется по формуле:

= + А;

,

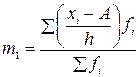где: - величина момента первого порядка;

- величина интервала;

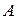- центральный вариант ряда (условный 0).