Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Обертальний рух твердого тіла
|
|
Під абсолютно твердим тілом розуміють нескінченну множину м.т., для якої відстань між двома довільними точками не зміниться при довільних рухах тіла.
Надалі під твердим тілом розумітимемо абсолютну твердість. При обертальному русі тв.тіла залишається нерухомою пряма, яка проведена в центрі тіла(вісь обертання). Будемо вв., що обертання здійснюється навколо закріпленої осі z. Вибиремо в тілі довільну т. М, положення якої в момент часу t визначається як  .
.

 . Т.
. Т.  знаходиться на колі.
знаходиться на колі.
Рух т.М може бути заданим за допомогою кута повороту  . Вектор миттєвого повороту визначається
. Вектор миттєвого повороту визначається 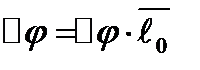 , де
, де  - орт вісі обертання. Напрямок вектора кутового переміщення
- орт вісі обертання. Напрямок вектора кутового переміщення  вибирають таким чином, що дивлячись з кінця цього вектора, рух спостерігався б проти напрямку руху годинникової стрілки.
вибирають таким чином, що дивлячись з кінця цього вектора, рух спостерігався б проти напрямку руху годинникової стрілки.  . З трикутника
. З трикутника 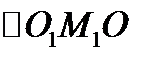 .
.  .
.  - рівнобедрений.
- рівнобедрений.  . Переміщення
. Переміщення  .
.  Визначимо миттєву швидкість
Визначимо миттєву швидкість 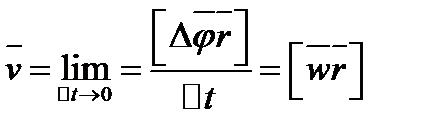 .
.  -миттєва кутова швидкість її напрямок співпадає з
-миттєва кутова швидкість її напрямок співпадає з  .
.  .
. 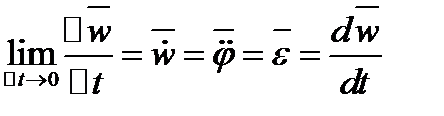 -вектор миттєвого прискорення, він співпадає з напрямом вісі обертання.
-вектор миттєвого прискорення, він співпадає з напрямом вісі обертання.  співпадають у випадку збільшення модуля
співпадають у випадку збільшення модуля  . Говорять, що при обертанні навколо закріпленої осі, тв.тіло має 1 ступінь рівності, і описується з допомогою 1 параметра.
. Говорять, що при обертанні навколо закріпленої осі, тв.тіло має 1 ступінь рівності, і описується з допомогою 1 параметра.
Розглянемо поступальний рух тв.тіла. При ньому залиш. паралельною сама собі довільна пряма, яка проведена вздовж тіла. Можна показати, що поступальний рух тв.тіла буде визначат. законом руху довільної точки цього тіла. Складний рух т.о. можна розглядати як комбінацію поступального та обертал. рухів.
8. При геометричному описі руху, яким займається кінематика, вибір системи відліку не обмежений будь-яким умовою. У принципі для опису руху можна користуватися будь-якими системами, але, щоб вони були доцільно вибрані.
Розглянемо нерухому систему коор-т К:  ,
,  . Нехай сис-ма
. Нехай сис-ма  рухається відносно системи К довільним чином
рухається відносно системи К довільним чином 

Через  позначимо радіус-вектор, який визначає положення точки М в нерухомій системі, через
позначимо радіус-вектор, який визначає положення точки М в нерухомій системі, через  '- радіус-вектор тієї ж точки в рухомій системі,
'- радіус-вектор тієї ж точки в рухомій системі,  - радіус-вектор початку координат рухомої системи в нерухомій. Між цими радіус-векторами для будь-якого моменту часу має місце:
- радіус-вектор початку координат рухомої системи в нерухомій. Між цими радіус-векторами для будь-якого моменту часу має місце:  (1).
(1).
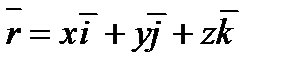 (2),
(2),  (3),
(3),  (4)
(4)
 ,
,  з одного боку, та
з одного боку, та  '- з іншого, вимірюються в різних системах. Розглянемо хід часу в рухомій системі. Момент часу, в який відбувається деяка подія, один і той же у всіх системах, тобто
'- з іншого, вимірюються в різних системах. Розглянемо хід часу в рухомій системі. Момент часу, в який відбувається деяка подія, один і той же у всіх системах, тобто
 З рівності випливає, що проміжки часу в різних системах між двома подіями однакові:
З рівності випливає, що проміжки часу в різних системах між двома подіями однакові:  .
.
Довжиною відрізка називається відстань між одночасними положеннями його кінців, виміряний накладенням масштабу в даній системі відліку.
Щоб отримати формулу додавання швидкостей треба про диференціювати
 по часу:
по часу:
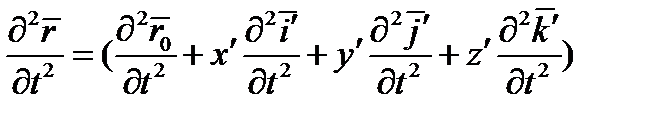 +
+  +
+ 
Ліва частина у цій рівності дає прискорення точки М в складеному рухові. У правій частині рівності вважаємо  постійними величинами. Тоді в правій частині
постійними величинами. Тоді в правій частині  . Вони і дають прискорення відносного руху:
. Вони і дають прискорення відносного руху:

 -поступальне прискорення
-поступальне прискорення
 -прискорення Коріоліса
-прискорення Коріоліса
 Отже, прискорення в складному русі дорівнює геометричній сумі трьох прискорень: переносного, відносного і прискорення Коріоліса:
Отже, прискорення в складному русі дорівнює геометричній сумі трьох прискорень: переносного, відносного і прискорення Коріоліса: 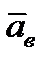 +
+  +
+  =
=