Розрахункові дані для рішення задачі №2.

Групи підприємств за вартістю основних фондів	Кількість підприємств
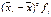
В цілому по сукупності		–			–	–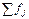

Перші дві графи таблиці заповнюються за даними інтервального ряду розподілу задачі №1.

Розрахунок середньої за згрупованими даними носить умовний характер, так як ґрунтується на припущенні, що в межах інтервалу індивідуальні значення ознаки розподіляються рівномірно.

Середню визначають за формулою середньої арифметичної зваженої:

,

де: - середнє значення ознаки ої групи, для кожної групи визначається як середнє значення інтервалу, тобто як півсума двох його меж;

частота -ої групи;

- число значень ознаки по сукупності в цілому.

Для характеристики варіації ознаки Х необхідно обчислити дисперсію, середнє квадратичне відхилення та квадратичний коефіцієнт варіації.

Дисперсія – це середній квадрат відхилень від середньої. Для згрупованих даних

,

або

Середнє квадратичне відхилення – це корінь квадратний із дисперсії

Коефіцієнти варіації розраховують як відношення абсолютних характеристик варіації до характеристики центру розподілу. Квадратичний коефіцієнт варіації обчислюють за формулою

Вважають, що сукупність є однорідною, а середня типовою, коли коефіцієнт варіації не перевищує 33%.

Вибіркова сукупність, яка обстежується є частиною генеральної сукупності з якої проводиться відбір ознак для спостереження.

Між характеристиками вибіркової сукупності і характеристиками генеральної сукупності, як правило існують деякі розходження, які називають помилкою вибірки.

Розмір граничної помилки вибірки залежить від варіації ознаки 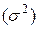, обсяг вибірки та її частини у генеральній сукупності , від прийнятого рівня ймовірності:

де квантиль нормального розподілу, довірче число (коефіцієнт довіри), який вказує як співвідносяться гранична і стандартна помилки вибірки для прийнятого рівня ймовірності;

- стандартна помилка вибірки, середнє квадратичне відхилення вибіркових оцінок від значень параметра генеральної сукупності.

В економічних розрахунках рекомендується використовувати довірчу ймовірність 1- або для яких квантиль відповідно складає 1.96 та 2.00.(додаток 1)

У теорії вибіркового методу розглядається два способи відбору: повторний і безповторний. При повторному відборі за схемою кулі, що повертається імовірність попасти в вибірку однакова для всіх елементів сукупності. При безповторному відборі за схемою кулі, що не повертається відібрана одиниця не повертається назад і ймовірність відбору окремих елементів весь час змінюється.

Використання випадкової повторної вибірки в практиці обмежено. Тому в задачі визначають середню квадратичну помилку випадкової безповторної вибірки за формулою:

де - обсяг вибірки;

- обсяг генеральної сукупності.

Довірчі межі генеральної середньої та частки визначають наступним чином:

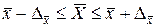
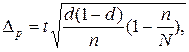
де гранична помилка вибіркової середньої;

- генеральна частка;

d - вибіркова частка;

гранична помилка вибіркової частки.

Моду розраховують за формулою

де нижня межа модального інтервалу;

h-ширина модального інтервалу;

відповідно частота модального, передмодального і післямодального інтервалів;

Медіану в інтервальному ряду знаходять за наступною формулою:

де відповідно нижня межа і ширина медіанного інтервалу;

сума накопичених частот в передмедіанному інтервалі;

частота медіанного інтервалу.

В задачі №3 передусім необхідно розрахувати абсолютні та відносні характеристики ряду динаміки.

Динамічний ряд - це послідовність чисел, які характеризують зміну того чи іншого соціально-економічного явища. Для динамічного ряду характерні перелік хронологічних дат або інтервалів часу і конкретні значення відповідних статистичних показників, які називають рівнями ряду.

Розрахунок характеристик рядів динаміки ґрунтується на зіставленні рівнів ряду :

Абсолютний приріст відображає абсолютну швидкість зміни рівнів ряду; розраховується як різниця рівнів динамічного ряду: