
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Розрахункові данні для обчислення характеристик кореляційного зв’язку.
|
|
| Групи підприємств | Кількість підприємств
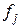
| 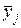
| 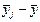
| 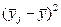
| 
|
| … В цілому по сукупності | …

| …
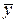
| … х | … х | …
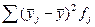
|
Міжгрупова дисперсія розраховується за формулою:

Загальна дисперсія
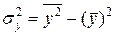
Середній квадрат 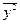 розраховується за вихідними даними задачі №1.
розраховується за вихідними даними задачі №1.
За статистичною структурою відношення 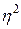 є частиною варіації результативної ознаки у, яка пов’язана з варіацією ознаки х. Перевірка істотності зв’язку між ознаками у і х проводиться за допомогою порівняння фактичних значень
є частиною варіації результативної ознаки у, яка пов’язана з варіацією ознаки х. Перевірка істотності зв’язку між ознаками у і х проводиться за допомогою порівняння фактичних значень 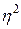 або критерію Фішера (F - критерію) з критичними значеннями.
або критерію Фішера (F - критерію) з критичними значеннями.
Якщо фактичні значення 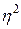 та F-критерію більше від критичних;
та F-критерію більше від критичних;

то зв’язок між результативною та факторною ознаками істотний. Критичні значення F і 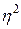 для рівня істотності a = 0.05 наводяться в додатках 3 і 4.
для рівня істотності a = 0.05 наводяться в додатках 3 і 4.
Розподіл 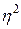 та F-критерію в таблицях залежить від числа ступіней міжгрупової
та F-критерію в таблицях залежить від числа ступіней міжгрупової  і середньої з групових
і середньої з групових 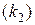 дисперсій:
дисперсій: 
де n, m – відповідно кількість елементів сукупності і груп.
Критерій Фішера обчислюють за формулою:
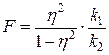
В другій частині задачі №8 необхідно оцінити лінію регресії за допомогою кореляційно - регресійного аналізу. У моделі регресійного аналізу характеристикою кореляційного зв’язку виступає теоретична лінія регресії, що описується функцією Y=F(x), яка називається рівнянням регресії. Лінійне рівняння регресії має вигляд Y= a + bx. Зі змінною х ознаки змінюється більш – менш рівномірно. Для обчислення параметрів рівняння регресії складають систему нормальних рівнянь:
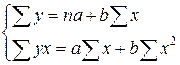
Розрахункові суми для складання системи нормальних рівнянь визначення коефіцієнта детермінації та кореляції послідовно заносять в табл.1.6.
Табл.1.6