
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Применение критерия Михайлова А.В. для анализа устойчивости линейных САР.
|
|
Тема № 9
Частотные критерии устойчивости.
План лекции № 9
9.1Частотные критерии устойчивости. Принцип аргумента.
9.2 Критерий устойчивости Михайлова А.В. Годограф Михайлова. Вещественная и мнимая функции Михайлова.
Применение критерия Михайлова А.В. для анализа устойчивости линейных САР.
9.1Частотные критерии устойчивости. Принцип аргумента.
Частотные критерии устойчивости.
Частотные критерии устойчивости используют связь между устойчивостью системы и формой ее частотных характеристик. Устойчивость САУ по виду частотных характеристик определяется с помощью частотных критериев, основанных на использовании принципа аргумента Коши, известного из теории функций комплексного переменного. Это критерии Михайлова, Найквиста и D -разбиения.
Полином  можно разложить на множители, тогда
можно разложить на множители, тогда  . Корни
. Корни 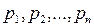 находятся из уравнения
находятся из уравнения  .
.
Принцип аргумента.
Частотные критерии устойчивости основываются на использовании принципа аргумента. Рассмотрим этот принцип, для чего характеристический полином замкнутой системы
 (9.1)
(9.1)
в соответствие с теоремой Безу представим в виде:
F(p) =  , (9.2)
, (9.2)
где – pi полюс передаточной функции замкнутой системы (  ).
).
Поставляя в выражение (9.1) вместо p комплексную переменную jω, получим:
 . (9.3)
. (9.3)
После аналогичной подстановки в выражение (9.2) получим:
F(jω) =  . (9.4)
. (9.4)
Каждому сомножителю  в выражении (9.4) на комплексной плоскости соответствует некоторый вектор, положение которого меняется при изменении ω.
в выражении (9.4) на комплексной плоскости соответствует некоторый вектор, положение которого меняется при изменении ω.
Определим изменение аргумента комплексной функции F(jω) при изменении частоты ω от до  . Для этого необходимо определить изменение аргумента каждого из векторов
. Для этого необходимо определить изменение аргумента каждого из векторов  , поскольку
, поскольку
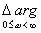 F(jω) = ∑ ∆ arg (jω – pi).
F(jω) = ∑ ∆ arg (jω – pi).

|
а) рi – действительный отрицательный полюс; б) рi - действительный положительный полюс; в) рi, рi +1- «левые» комплексно сопряженные полюса; г) рi, рi +1- «правые» комплексно сопряженные полюса;
Рис 9.1 К оценке изменения аргумента сомножителя (jω -рi)
Если корень характеристического уравнения pi действительный и отрицательный, т.е. расположен на действительной оси слева от начала координат (рис. 9.1, а), то вектор  поворачивается против часовой стрелки на угол π /2, если этот корень действительный и положительный (рис. 9.1, б), то вектор поворачивается по часовой стрелке на угол π /2. Следовательно, для левого действительного полюса
поворачивается против часовой стрелки на угол π /2, если этот корень действительный и положительный (рис. 9.1, б), то вектор поворачивается по часовой стрелке на угол π /2. Следовательно, для левого действительного полюса
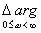
 = π /2,
= π /2,
а для правого действительного полюса
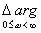
 = – π /2,
= – π /2,
Нетрудно показать, что для пары комплексно сопряженных левых полюсов (рис. 9.1, в) изменение аргумента составляет +π, а для пары комплексно сопряженных правых полюсов (рис. 9.1, г) равно -π.
Если среди n полюсов передаточной функции замкнутой системы m расположены справа от мнимой оси, а остальные (n – m)– слева, то изменение аргумента комплексной функции F(jω) вектора равно:
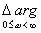 F(jω) = (n – m)∙ π /2 – m ∙ π /2 = (n – 2 m)∙ π /2. (9.5)
F(jω) = (n – m)∙ π /2 – m ∙ π /2 = (n – 2 m)∙ π /2. (9.5)
Выражение (9.5) и определяет суть принципа аргумента. В передаточной функции устойчивой системы правые полюса отсутствуют, т.е. m = 0, и изменение аргумента F(jω) равно:
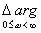 F(jω) = n ∙ π /2. (9.6)
F(jω) = n ∙ π /2. (9.6)
На комплексной плоскости каждому корню соответствует определенная точка. Подставив 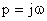 , получаем
, получаем
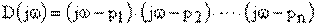 . (9.7)
. (9.7)
Каждый вектор  может быть представлен в виде вектора, начало которого лежит в точке, определяющей корень
может быть представлен в виде вектора, начало которого лежит в точке, определяющей корень 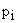 а конец лежит на мнимой оси. Следовательно,
а конец лежит на мнимой оси. Следовательно,  можно представить суммарным вектором, равным произведению элементарных векторов. Модуль суммарного вектора будет равен произведению модулей отдельных векторов, а фаза – сумме фаз этих векторов. При изменении частоты конец каждого вектора будет перемещаться вдоль мнимой оси. При изменении частоты от
можно представить суммарным вектором, равным произведению элементарных векторов. Модуль суммарного вектора будет равен произведению модулей отдельных векторов, а фаза – сумме фаз этих векторов. При изменении частоты конец каждого вектора будет перемещаться вдоль мнимой оси. При изменении частоты от  до
до  каждый составляющий вектор, начало которого лежит на вещественной оси, повернется на угол, равный
каждый составляющий вектор, начало которого лежит на вещественной оси, повернется на угол, равный 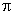 , если его начало лежит в левой полуплоскости, и равный –
, если его начало лежит в левой полуплоскости, и равный – 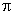 , если его начало лежит в правой полуплоскости. Каждая пара комплексно-сопряженных корней – соответственно на угол +
, если его начало лежит в правой полуплоскости. Каждая пара комплексно-сопряженных корней – соответственно на угол + 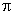 .
.
Если характеристическое уравнение имеет m корней в правой полуплоскости, то в левой полуплоскости число этих корней будет равно n-m. При изменении частоты от  до
до  суммарный угол поворота вектора характеристического полинома определяется как
суммарный угол поворота вектора характеристического полинома определяется как
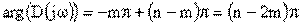 . (9.8)
. (9.8)
Для устойчивости САУ необходимо и достаточно, чтобы все корни характеристического уравнения лежали в левой полуплоскости, то есть чтобы  . Таким образом, если вектор характеристического полинома замкнутой САУ порядка " n" при изменении частоты от
. Таким образом, если вектор характеристического полинома замкнутой САУ порядка " n" при изменении частоты от  до
до  описывает в положительном направлении угол n
описывает в положительном направлении угол n 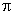 , то такая система регулирования будет устойчива. В противном случае САУ будет неустойчива.
, то такая система регулирования будет устойчива. В противном случае САУ будет неустойчива.
В силу симметричности кривой, описываемой концом вектора характеристического полинома, можно ограничиться рассмотрением лишь ее части, соответствующей положительным значениям частоты. При этом угол, описываемый вектором характеристического полинома при изменении частоты от 0 до  , уменьшится вдвое и будет определяться как
, уменьшится вдвое и будет определяться как
 .
.
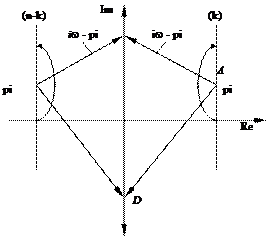
Рассмотрим комплексную плоскость  (рисунок 9.2), на которой точками отмечены корни
(рисунок 9.2), на которой точками отмечены корни  .
.
 | |||
 | |||
Рисунок 9.2 Расположение корней на комплексной плоскости 
Предположим, что первые  из этих корней лежат справа от мнимой оси, а остальные (
из этих корней лежат справа от мнимой оси, а остальные ( ) корней - слева от мнимой оси. Пусть теперь независимая переменная
) корней - слева от мнимой оси. Пусть теперь независимая переменная  меняется вдоль мнимой оси от минус
меняется вдоль мнимой оси от минус  до
до  , т.е.
, т.е.  , где
, где  . Пусть точка
. Пусть точка 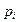 лежит справа от мнимой оси. Построим разность
лежит справа от мнимой оси. Построим разность  , которая изображена на рисунке 2 вектором
, которая изображена на рисунке 2 вектором 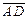 . При изменении
. При изменении  от минус
от минус  до
до  вектор
вектор 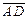 повернется вокруг точки
повернется вокруг точки  на угол минус
на угол минус  (направленное вращение по часовой стрелке будем считать отрицательным). Таким образом, если корень
(направленное вращение по часовой стрелке будем считать отрицательным). Таким образом, если корень 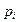 лежит справа от мнимой оси, то приращение аргумента числа
лежит справа от мнимой оси, то приращение аргумента числа  при изменении
при изменении  от минус
от минус  до
до  равно минус
равно минус  . Если корень
. Если корень 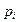 лежит слева от мнимой оси, то приращение аргумента числа
лежит слева от мнимой оси, то приращение аргумента числа  при изменении
при изменении  от минус
от минус  до
до  равно
равно  . Приращение аргумента функции
. Приращение аргумента функции  равно
равно
 .
.
Отсюда при изменении  от минус
от минус  до
до  получим
получим

Необходимое и достаточное условие устойчивости состоит в том, что  , поэтому для устойчивости системы необходимо и достаточно, чтобы
, поэтому для устойчивости системы необходимо и достаточно, чтобы  .
.  сопряжено с минус
сопряжено с минус  , т.е.
, т.е.  = -
= -  , поэтому годограф
, поэтому годограф  симметричен годографу
симметричен годографу  относительно действительной оси
относительно действительной оси  -плоскости, отсюда
-плоскости, отсюда  и, следовательно, для устойчивости САУ необходимо и достаточно выполнение условия
и, следовательно, для устойчивости САУ необходимо и достаточно выполнение условия  .
.
9.2 Критерий устойчивости Михайлова А.В. Годограф Михайлова. Вещественная и мнимая функции Михайлова.
Критерий устойчивости Михайлова основан на рассмотрении характеристического многочлена  , но имеющего несколько иное представление. Подставим в этот многочлен
, но имеющего несколько иное представление. Подставим в этот многочлен  . В результате получим комплексную функцию
. В результате получим комплексную функцию  .
.
Из выражения (9.6) следует критерий устойчивости Михайлова, согласно которому изменение аргумента комплексной функции Q(jω) определяется по годографу, который записывают в виде
Q(jω) = U(ω) + jV(ω),
где U(ω), V(ω) – действительная и мнимая составляющие комплексной функции Q(jω);
U(ω) = a 0 – a 2 ω 2 + a 4 ω 4 – a 6 ω 6 + ……;
V(ω) = a 1 ω – a 3 ω 3 + a 5 ω 5 – a 7 ω 7 + …….
Критерий Михайлова – это частотный критерий, позволяющий судить об устойчивости замкнутой системы по поведению ее характеристического вектора на комплексной плоскости.
Вещественная часть  получена из членов многочлена
получена из членов многочлена  , содержащих четные степени
, содержащих четные степени  , а мнимая часть
, а мнимая часть  получена из членов
получена из членов  с нечетными степенями
с нечетными степенями  . Функция
. Функция  отображается в виде годографа на комплексной плоскости (рисунок 9.3). Этот годограф называют годографом Михайлова. Каждому значению
отображается в виде годографа на комплексной плоскости (рисунок 9.3). Этот годограф называют годографом Михайлова. Каждому значению  соответствуют определенные значения
соответствуют определенные значения  и
и  и определенная точка на комплексной плоскости. При
и определенная точка на комплексной плоскости. При  функция
функция  , т.е. годограф начинается на действительной оси. При
, т.е. годограф начинается на действительной оси. При 

Если задаваться различными значениями  и откладывать значения
и откладывать значения  по горизонтальной, а
по горизонтальной, а  – по вертикальной осям декартовой системы координат, то будет получена кривая, называемая годографом характеристического вектора или годографом Михайлова. Другая формулировка: годографом Михайлова называется множество точек, образованных при движении характеристического вектора САУ при изменении частоты от 0 до
– по вертикальной осям декартовой системы координат, то будет получена кривая, называемая годографом характеристического вектора или годографом Михайлова. Другая формулировка: годографом Михайлова называется множество точек, образованных при движении характеристического вектора САУ при изменении частоты от 0 до  .
.
То есть для устойчивости САУ необходимо выполнение условия вида:
 . (9.9)
. (9.9)
Формулировка критерия: для устойчивости системы необходимо и достаточно, чтобы ее характеристический вектор при изменении частоты от 0 до  повернулся в положительном направлении (против часовой стрелки), начиная с положительной вещественной оси на число квадрантов, равное порядку характеристического уравнения.
повернулся в положительном направлении (против часовой стрелки), начиная с положительной вещественной оси на число квадрантов, равное порядку характеристического уравнения.
На рис. 9.3 годограф 1 относится к устойчивой САУ, годографы 3, 4. 5, 6, 7 - к неустойчивой САУ. Если годограф проходит через начало координат (кривая 2 на рис. 9.3), то система находится на границе устойчивости. Действительно, в этом случае существует значение  , при котором
, при котором  , т.е. характеристическое уравнение системы, имеет пару сопряженных мнимых корней
, т.е. характеристическое уравнение системы, имеет пару сопряженных мнимых корней  . А это и означает наличие в системе незатухающих колебаний, т.е. нахождение ее на границе устойчивости. Незначительное изменение параметров системы, в результате которого годограф
. А это и означает наличие в системе незатухающих колебаний, т.е. нахождение ее на границе устойчивости. Незначительное изменение параметров системы, в результате которого годограф  на рис. 9.3 отойдет влево от начала координат, делает систему устойчивой, а изменение параметров в другую сторону - неустойчивой.
на рис. 9.3 отойдет влево от начала координат, делает систему устойчивой, а изменение параметров в другую сторону - неустойчивой.
 |
Рис. 9.3- Годограф Михайлова
Примеры годографов Михайлова для устойчивых САУ разных порядков (от  до
до  ) изображены на рис. 6.9
) изображены на рис. 6.9
 |
Рис. 9.4 - Годографы Михайлова для устойчивых САУ