Вещественная и мнимая функции Михайлова

При построении годографа прежде всего находят точки его пересечения с осями координат. Для этого, определив из уравнения значения частот, соответствующих точкам пересечения годографа с мнимой осью, подставляют их в выражение . В результате получают соответствующие ординаты. Аналогично находят точки пересечения с действительной осью, приравнивая к нулю мнимую часть . Как видно из рисунка 9.4, годограф устойчивой системы имеет такой вид, что действительная и мнимая части функции должны строго по очереди обращаться в нуль, причем должна обращаться в нуль раз, если - четное, раз, если - нечетное число, т.е. 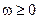должна иметь при , соответственно, или корней. Мнимая часть должна обращаться в нуль раз, если - четное, раз, если - нечетное число, т.е. 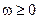должна иметь при , соответственно, или корней.

При переходе годографа из одного квадранта в другой попеременно обращаются в нуль его вещественная и мнимая части. Отсюда вытекает следствие из критерия Михайлова, заключающееся в том, что для устойчивой системы корни уравнений U (w) = 0 и V (w) = 0 должны чередоваться (условие перемежаемости корней) и общее число этих корней должно быть равно порядку характеристического полинома.

Таким образом, условие перемежаемости корней и можно принять за новый критерий устойчивости (рисунок 9.5).

а) б)

Рисунок 9ю5 Условия перемежаемости корней: выполняется (а), не выполняется (б)

Для устойчивости системы необходимо и достаточно, что бы корни функций и строго перемежались. Критерий Михайлова в этой форме иногда называют критерием перемежаемости корней.

На рисунке 9.6, а показана кривая Михайлова неустойчивой сис­темы, у которой нарушена последовательность обхода квадрантов комплексной плоскости. Система находится на апериодической гра­нице устойчивости (рисунок 9.6, б), если кривая при w = 0 начинается в начале координат, и на периодической границе устойчивости, если кривая при w ¹ 0 проходит через начало координат. Заметим, что обо­значения осей U (ω) и V (ω) обычно используются при построении час­тотных характеристик на комплексной плоскости не по всей переда­точной функции, а лишь по ее знаменателю.

а б в

Рисунок 9.6

Число правых корней характеристического уравнения можно определить по формуле , где – это полное приращение аргумента характеристической функции (суммарный угол поворота). Вектор D (j ω) системы пятого порядка (рисунок 9.6, в) сначала поворачивается на угол 3·(π /2) или три квад­ранта против часовой стрелки, затем возвращается на угол 2·(π /2) или два квадранта по часовой стрелке, что в итоге соответствует полному приращению = π /2. Отсюда число правых корней m равно 5/2–1/2=2 (числу неправильных пересечений кривой осей координат).

Характеристическая кривая всегда начинается в точке на дейст­вительной оси, удаленной от начала координат на величину a_n. По­этому, если k входит только в свободный член a_n уравнения D(s) = 0, то критические значения k_{к р} определяются из графика при нулевом значении мнимой координаты V(w) = 0: апериодическая граница по условию a_n = 0, периодическая граница по a_n = |x| + y (рисунок 9.6, а).

Очевидно, что при нарушении очередности пересечения функ­циями оси абсцисс (частот) система неустойчива (рисунок 9.7, а). Сис­тема находится на апериодической границе устойчивости (рисунок 9.7, б), если обе функции начинаются в начале координат, и на периодиче­ской границе устойчивости (рисунок 9.7, в), если при w ¹ 0 кривые пе­ресекают ось частот в одной точке. В остальном диапазоне изменения функций условия устойчивости при этом не должны нарушаться. Час­тота w, при которой система находится на периодической границе ус­тойчивости, равна частоте незатухающих колебаний.

а б в г

Рисунок 9.7

На графике с кривой Михайлова обязательно должен указывать­ся порядок системы n, так как при его отсутствии может быть сделан ошибочный вывод.

9.3 Применение критерия Михайлова А.В. для анализа устойчивости линейных САР.

Рассмотрим на примере №1 применение критерия Михайлова А.В. для анализа устойчивости линейной САР, структурная схема которой приведена на рис. 9.8. Здесь

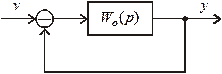
Рис.9.8. Структурная схема исследуемой системы

.

Определим передаточную функцию замкнутой системы

и запишем ее характеристический полином

перейдем к выражению для годографа Михайлова

и представим его в форме

С целью построения годографа Михайлова вычислим значения вещественной и мнимой частей при конкретных значениях частоты и занесем их в таблицу.

			1, 22	1, 41
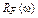
				–1
			0, 61

По данным таблицы построим годограф Михайлова.

Как видим из рис. 9.9, он проходит последовательно три квадранта, не обращаясь в нуль и стремясь к бесконечности в третьем квадранте. Следовательно, система устойчива.

Пример №2. Проверить устойчивость системы, структурная схема которой приведена на рис.9.10. Данная система представляет собой упрощенную модель одного из сочленений руки робота-манипулятора. Исполнительным механизмом является двигатель постоянного тока, а соединение с рукой осуществляется через редуктор.

Рис. 9.10. Структурная схема руки робота

Здесь – напряжение, подаваемое на якорь двигателя; – угловая скорость вращения двигателя; 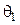– угол поворота вала двигателя; – угол поворота руки. При отсутствии возмущений взаимосвязь между скоростью вращения двигателя и входным напряжением 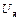определяет передаточная функция , а угол поворота вала двигателя связан с его угловой скоростью вращения зависимостью . Ей соответствует на схеме вторая передаточная функция . Редуктор представляет собой безынерционное звено с передаточной функцией , где r – передаточное отношение редуктора.

Проверим устойчивость системы при следующих значениях параметров передаточных функций: , . Определим общую передаточную функцию сочленения руки робота

и запишем характеристический полином

выражение для годографа Михайлова

представим в форме

Поскольку при вещественная и мнимая части одновременно обращаются в нуль, годограф Михайлова начинается в начале координат. Это означает, что система находится на границе устойчивости.