Критерий Г.Найквиста для исследования устойчивости астатических систем.

Второй случай охватывает нейтральные САУ, т.е. находящиеся в разомкнутом состоянии на границе устойчивости. Таким свойством обладают астатические САУ, ПФ которых в общем случае имеют вид оператора (3.32), а годограф W (j w) не может образовать замкнутого контура ни с одной из осей, так как начинается (w = 0) в бесконечности. Эту особенность называют разрывом годографа.

Во втором случае критерий Найквиста формулируется следующим образом: для устойчивости замкнутой САУ необходимо и достаточно, чтобы годограф разомкнутой САУ, дополненный на участке разрыва дугой бесконечно большого радиуса, не охватывал критическую точку.

На рисунке 10.5 показаны годографы 1 и 2 САУ с астатизмом первого порядка (v = 1). Годограф 1 принадлежит устойчивой, а годограф 2 – неустойчивой системе.

Клювообразный годограф на ри­сунке 10.6 принадлежит устойчивой САУ с астатизмом второго порядка (v = 2).

Третий случай охватывает САУ, неустойчивые в разомкнутом состоя­нии. Характеристический полином таких систем A (s) имеет l " правых" корней, т.е. корней с положительной вещественной частью.

В третьем случае, наиболее общем, критерий Найквиста формулируется следующим образом: для устойчивости замкнутой САУ необходимо и достаточно, чтобы годограф разомкнутой САУ охватывал критическую точку l /2 раз в положительном направлении (против часовой стрелки).

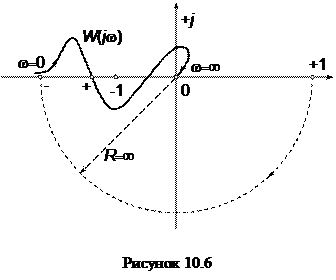Анализ устойчивости САУ с годографом сложной формы, например изобра­женным на рисунке 10.6, упрощается при использова­нии правила переходов. Критерий Найквиста форму­лируется при этом следую­щим образом: замкнутая САУ устойчива, если раз­ность между количеством положительных и отрица­тельных переходов годогра­фа разомкнутой системы W (j w) через отрезок вещественной оси от -¥ до критической точки равна l /2. Годограф может начинаться на указанном отрезке при w = 0 (рисунок 10.6) или заканчиваться при w = ¥. В этом случае считают, что годограф совершает полперехода. Так, например, годограф, изображенный на рисунке 10.6, совершает один положительный переход, отмеченный знаком " +", и половину отрицательного перехода, отмеченного знаком " -". Разность названных переходов равна +1/2. Замкнутая САУ будет устойчивой, если l /2 = 1/2.

Если характеристический полином разомкнутой системы A (s) кроме корней с вещественной частью имеет нулевые и чисто мнимые корни, то на участках разрыва годограф W (j w) должен быть дополнен дугой бесконечно большого радиуса.

Обычная формулировка критерия (рисунок 10.7):

Система, устойчивая в разомкнутом состоянии или нейтраль­ная, будет устойчивой в замкнутом состоянии, если ее АФЧХ при из­менении частоты w от нуля до плюс бесконечности не охватывает точку с координатами (-1, j0).

а б

Рисунок 10.7

Критерий Найквиста формулируется следующим образом: если характеристическое уравнение разомкнутой системы порядка имеет корней в правой полуплоскости и () корней в левой полуплоскости (), то для устойчивости системы в замкнутом состоянии необходимо и достаточно, чтобы годограф АФХ разомкнутой системы охватывал точку () на угол .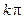

Здесь требуется уточнить, что понимается под термином «годограф АФХ охватывает точку ()». Годографы, с которыми обычно приходится иметь дело, имеют некоторое начало при и конец при .

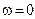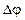Проведем из точки к некоторой точке вектор (рис.10.8). Заставим теперь мысленно точку пробежать весь годограф от начала () до конца (). При этом аргумент вектора получит приращение и мы считаем, что годограф вектора охватывает точку на угол . Если , то говорим, что годограф не охватывает точку ().

Рис. 10.8 - Определение охвата годографом АФХ критической точки

Говоря про замыкание системы, подразумевают ее замыкание единичной ООС. АФЧХ называют также годографом Найквиста или годографом комплексного коэффициента передачи W(jw). Отрица­тельные, мнимые или комплексные частоты, получающиеся в резуль­тате расчетов, при построении АФЧХ отбрасывают, и ветвь годографа Найквиста для диапазона частотwот 0 до -∞ обычно не строят.

Годограф нейтральной в разомкнутом состоянии системы с ПФ вида W(s) = W₀(s)/sⁿ дополняется дугой n(-p/2) бесконечного радиуса, начинающейся на положительной действительной полуоси. Здесь n – степень астатизма системы (число нулевых корней в знаменателе пе­редаточной функции), если n ¹ 0, то годограф Найквиста при w = 0 начинается в бесконечности (рисунок 10.7, б).

Замкнутая система находится на апериодической границе ус­тойчивости, если при w = 0 годограф Найквиста начинается в точке
(-1, j 0), и на периодической границе устойчивости, если при w ¹ 0 го­дограф проходит через точку (-1, j 0).

Особая роль точки (-1, j 0) заключается в том, что она:

а) указывает на превращение ООС в ПОС, т.е. соответствует моменту изменения знака фазы сигнала в цепи обратной связи, пере­ходу отставания в опережение по фазе;

б) является границей между режимами усиления (k> 1) и ослаб­ления (k< 1) сигнала. Считая D_зам(s) = 1 + W_раз(s) = 0, получаем кри­тическое значение W_раз(s) = - 1.

Универсальная (общая) формулировка критерия Найквиста учи­тывает и случаи, когда разомкнутая система неустойчива.

Замкнутая система устойчива, если сумма переходов АФЧХ ра­зомкнутой системы отрезка ]-¥, -1[ при увеличении частоты w от нуля до плюс бесконечности равна p/2, где p – число правых корней характеристического уравнения разомкнутой системы.

Иначе говоря, система будет устойчивой после замыкания, если АФЧХ охватывает точку (-1, j 0) против часовой стрелки на угол p ∙ π.

Рисунок 10.9	АФЧХ, имеющую несколько пе­ресечений с отрезком ]-¥, -1[, называ­ют АФЧХ II-го рода (рисунок 10.9) в от­личие от простой АФЧХ I-го рода. Пе­реход на интервале -∞ < Re (ω) < -1 сверху вниз считают положительным, снизу вверх – отрицательным.

Если АФЧХ начинается или заканчивается на критическом от­резке ]-¥, -1[, исключая точки -∞ и -1, то считают, что АФЧХ совер­шает ½ перехода. При единственном правом полюсе замкнутая систе­ма устойчива, если АФЧХ разомкнутой системы начинается на крити­ческом отрезке и уходит вниз, совершая ½ положительного перехода.