
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Свойства корня n-ой степени.
|
|
Теорема 1. Корень n-й степени(2, 3, 4…) из производных 2-х неотрицательных чисел равен произведений корней n-й степени из этих чисел.
 =
=  *
*  ;
;
Теорема остается справедливой и для случая, когда подкоренное выражение представляет собой произведение более чем двух неотрицательных чисел.
Теорема 2. Если a  0, b
0, b  0 и n-натуральное число, больше 1, то справедливо равенство:
0 и n-натуральное число, больше 1, то справедливо равенство:  =
= 
Краткая (хотя и неточная) формулировка, которую удобнее использовать на практике: корень из дроби равен дроби от корней.
Теорема позволяет нам перемножать т олько корни одинаковой степени, т.е. только корни с одинаковым показателем.
Теорема 3. Если a  0, k-натуральное число и n-натуральное, больше 1, то справедливо равенство:
0, k-натуральное число и n-натуральное, больше 1, то справедливо равенство:
 =
= 
Иными словами, чтобы возвести корень в натуральную степень, достаточно возвести в эту степень подкоренное выражение.
Это — следствие теоремы 1. В самом деле, например, для к = 3 получаем:
 =
=  *
*  *
*  =
=  =
=  . Точно так же можно рассуждать в случае любого другого натурального значения показателя к.
. Точно так же можно рассуждать в случае любого другого натурального значения показателя к.
Теорема 4. Если a  0 k, n-натуральное числа, больше 1, то справедливо равенство:
0 k, n-натуральное числа, больше 1, то справедливо равенство:
 =
=  ;
;
Иными словами, чтобы извлечь корень из корня, достаточно перемножить показатели корней.
Например,  =
=  ;
; 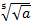 =
=  ;
;  =
=  .
.
Будьте внимательны! Мы узнали, что над корнями можно осуществлять четыре операции: умножение, деление, возведение в степень и извлечение корня (из корня). А как же обстоит дело со сложением и вычитанием корней? Никак.
Например, вместо 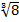 + 27 нельзя написать
+ 27 нельзя написать 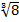 +
+  . В самом деле,
. В самом деле,
В самом деле,  , a
, a 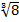 +
+  = 2+3=5. Но ведь очевидно, что
= 2+3=5. Но ведь очевидно, что 
 5
5
Теорема 5. Если показатели корня подкоренного выражения умножить или разделить на одно и то же натуральное число, то значение корня не изменится, т.е.  =
=  .
.
4, 5.ОСНОВНЫЕ СВОЙСТВА ЛОГОРИФМОВ.
-  – логарифм числа b по основанию a (a
– логарифм числа b по основанию a (a  0, a
0, a  1, b
1, b 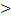 0);
0);
-  - десятичный логарифм (логарифм по основанию 10, a=10);
- десятичный логарифм (логарифм по основанию 10, a=10);
-  – натуральный логарифм (логарифм по основанию e, a=e).
– натуральный логарифм (логарифм по основанию e, a=e).
Формулы и свойства логарифмов:
Для любых a; a> 0; a  1 и для любых x; y> 0.
1 и для любых x; y> 0.
 = b- основание логарифмическое тождество;
= b- основание логарифмическое тождество;
1)  = 0,
= 0,
2) 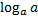 = 1,
= 1,
3)  =
=  +
+  ,
,
4)  =
=  -
-  ,
,
5) 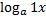 = -
= -  ,
,
6)  = p
= p  ,
,
7) 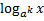 = 1k
= 1k  , при k
, при k  0,
0,
8)  =
=  ,
,
9)  =
=  – формула перехода к новому основанию,
– формула перехода к новому основанию,
10)  =
=  .
.
6.ФУНКЦИЯ у =  , ЕЁ СВОЙСТВА И ГРАФФИК.
, ЕЁ СВОЙСТВА И ГРАФФИК.
Квадратичная функция – это функция, которую можно задать формулой вида
y = ax 2 + bx + c,
где x – независимая переменная, a, b и c – некоторые числа, причём а ≠ 0.
Областью определения квадратичной функции является множество всех чисел. (Напомним: областью определения функции называется совокупность значений независимой переменной)
Функция y = ax2.
Функция y = ax 2 – это частный случай квадратичной функции.
Графиком функции y = ax 2 является парабола.
Свойства функции y = ax 2 при a > 0:
1. Если x = 0, то y = 0.
График функции проходит через начало координат.
2. Если x ≠ 0, то y > 0.
График функции расположен в верхней полуплоскости.
3. Противоположным значениям аргумента соответствуют равные значения функции.
Пояснение: допустим, x = –2, y = 8. При x = 2 значение y не меняется и составляет 8.
4. В промежутке (–∞; 0] функция убывает, а в промежутке [0; +∞) - возрастает.
5. Наименьшее значение функции равно нулю. Это значение она принимает при x = 0.
Наибольшего значения функция не имеет. Т.е. областью значений функции является промежуток [0; +∞).
Свойства функции y = ax 2 при a < 0:
1. Если x = 0, то y = 0.
График функции проходит через начало координат.
2. Если x ≠ 0, то y < 0.
График функции расположен в нижней полуплоскости.
3. Противоположным значениям аргумента соответствуют равные значения функции.
График функции представляет собой симметричную фигуру относительно оси y.
Пояснение: допустим, x = –4, y = –8. При x = 4 значение y не меняется и составляет –8.
4. В промежутке (–∞; 0] функция возрастает, а в промежутке [0; +∞) - убывает.
5. Наибольшее значение функции равно нулю. Это значение она принимает при x = 0.
Наименьшего значения функция не имеет. Т.е. областью значений функции является промежуток (–∞; 0].
7.ФУНКЦИЯ y=  , ЕЁ СВОЙСТВА И ГРАФИК.
, ЕЁ СВОЙСТВА И ГРАФИК.
Определение.Квадратным корнем из неотрицательного числа “a” называется такое неотрицательное число “b”, квадрат которого равен “a”.
{  = b --- {
= b --- {  = a
= a
{a  0 --- {b≥ 0
0 --- {b≥ 0
Свойства функции:
1. Область определения функции является луч [0; +∞);
2. y=0 при х=0 из этого следует что начало координат принадлежит графику функции; y> 0 при x> 0, а значит график располагается в первой координатной четверти (первом координатном угле)
3. Функция возрастает на луче [0; +∞); Другими словами на этом луче, большему значению аргумента, соответствует большее значение функции.
4. Функция имеет наименьшее значение, и не имеет наибольшего значения. Данное значение достигается тогда, когда х=0;
5. Функция непрерывна.
6. Функция выпукла вверх.
7. Область значений функции y=√ x является луч [0; +∞)
Следует отметить, что график функции y=√ x симметричен относительно оси симметрии у=х с графиком функции y=x^2, при x> 0. Этот факт отражен на рисунке ниже.
8.ФУНКЦИЯ y=  , ЕЁ СВОЙСТВА И ГРАФИК.
, ЕЁ СВОЙСТВА И ГРАФИК.
Функцию, заданную формулой y =  , называют логарифмической функцией с основанием a.
, называют логарифмической функцией с основанием a.
(a > 0, a ≠ 1)
Основные свойства логарифмической функции:
1. Область определения логарифмической функции - множество всех положительных чисел. D (f)=(0; +∞);
2. Множество значений логарифмической функции - множество R всех действительных чисел. E (f)=(− ∞; +∞);
3. Логарифмическая функция на всей области определения возрастает при a > 1 или убывает при 0< a < 1.
Логарифмическая функция не является ни четной, ни нечетной;
не имеет ни наибольшего, ни наименьшего значений;
не ограничена сверху, не ограничена снизу;
График любой логарифмической функции y = y =  проходит через точку (1; 0).
проходит через точку (1; 0).