Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Применение производной к исследованию функций на монотонность.
|
|
Если функция возрастает на промежутке и имеет на нем производную, то производная неотрицательна; если функция убывает на промежутке и имеет на нем производную, то производная не положительна.
Монотонно возрастающая функция – это функция, у которой большему значению аргумента соответствует большее значение функции.
Монотонно убывающая функция – это функция, у которой большему значению аргумента соответствует меньшее значение функции.
Выясняется, что функция возрастает на интервалах, где производная больше нуля:
f’(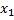
) = tg 
> 0 => f() 
;
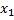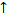Если же значение производной отрицательное, то функция убывает:
f’(
) = tg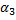 
< 0 => f() 
;
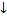Вся ОДЗ состоит из отдельных точек, значит, надо выделить те интервалы, на которых производная меньше нуля, на которых производная больше нуля, и они определят те участки ОДЗ, на которых функция либо возрастает, либо убывает. Этот же вывод мы получим, рассматривая соотношение △ y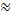 
f’(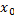
)*△ x. На тех областях, на которых производная f’(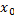) меньше нуля, △ y < 0 функция убывает. Соответственно, на тех областях ОДЗ, где производная f’(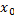) больше нуля, △ y < 0 функция возрастает.