Рыночные математические характеристики.

Введём в наше рассмотрение случайный характер финансовых событий. Наше ФС может совершится в другое время в другом объёме

Случайная величина это величина, которая. Воперых событий очень много, они различаются малыми отличиями. Большая часть событий происходит вне нашего.

Случайное событие. СС это событие возможность которого мы знаем он может произойти, а может не произойти при повторении может произойти, а может не произойти.

Если мы воспроизводим некоторый опыт при повторяющихся обстоятельствах, то мы обнаружим, что при этом происходят несколько однородных событий, но различающихся количественными параметрами. Например нам передали для проверки N=100 рефератов студентов. Мы точно знаем, что работы помещены в папки, в которых может быть 20, 30, 40, и 50 страниц. Однако когда мы перебираем работы по порядку, мы не знаем, сколько и каких работ в общей стопке и когда появится та или иная работа. Появление одной из работ студентов это поток однородных событий, но такая количественная характеристика, как количество страниц, заранее не известна. Кое -что мы знаем заранее, например, что как бы мы не перебирали работы, их всегда будет 100. Далее когда мы рассортируем все работы, окажется, что они все разложились на 4 стопки по 20, 30, 40, и 50 страниц, но удивительно что сложив количество работ, разбитых по толщине мы снова получим число N=100. Обозначим через n(20) число работ по 20 страниц, через n(30) число работ по 30 стр., n(40)- 40 стр. и n(50)- 50 стр. Наша формула даст n(20)+n(30)+n(40)+n(50)=100. Число таких однородных, но разных по количественным характеристикам может быть очень большим и даже бесконечным. Для удобства математической обработки таких выборок введено понятие вероятности события, нашим событием будет появление работы с 30 стр. или 20 стр. или 40 стр. или 50 стр.

Насколько часто появятся работы с 30 стр?. Рассмотрим n (30): это количество работ по 30 стр. котрые нам встретятся из общего числа 100. Чтобы определить долю n(30) от 100 шт. разделим n(30)/100 и получим, как часто появятся такие работы при проверке. Аналогично, то же можно проделать со всеми остальными стопками. Обозначим значение n(30)/100 через p(30) и назовём данное число вероятностью события появления работы с 30 стр. Также мы поступим с другими работами. Для полного набора событий характерна нормировка: Сумма вероятностей равна 1. Если наша подборка не даёт единицы, то надо искать пропавшие события. Если бы разброс числа страниц был бы шире, а работ больше, нам пришлось разбить подборку не на 4 группы, а на большее количество.В общем случае количество различных событий обозначим через k, и пронумеруем события параметром i. Тогда событие под номером i получит количественную характеристику p(i) называемую вероятностью события i. Напомню, число событий может быть бесконечно много и их значения могут располагаться бесконечно близко друг к другу. Такое распределение событий называется непрерывным. Как правило, для удобства рассмотрения различных событий составляющих полный набор (Сумма вероятностей равна 1) весь диапазон значений разбивают на большее или меньшее количество групп, начиная с наименьшего и до наибольшего. Например, если бы количество страниц в рефератах колебалось от 0 до 50, мы разбили бы весь диапазон на такие группы: (0-20); (21-30); (31-40); и (41-50). Теперь под событием мы понимаем попадание в диапазон от.... и до.... Тогда число рефератов с числом страниц от 21 и до 39 включительно составило бы, например, 23 штуки т.д.. Ясно, что рефераты распределились бы примерно так, как мы распределили их ранее. Число групп можно конечно варьировать для удобства описания.

Соотношение событий графически можно изобразить в виде диаграммы следующего вида

где по горизонтальной оси распределяются события по группам (так как мы их разбили), а по вертикальной частота появления. Для непрерывного распределения по горизонтальной оси откладывается значение изучаемой величины, а по вертикали- функция называемая плотность вероятности. В случае с непрерывной величиной для нормировки принимают требование, чтобы интеграл от f(x) dx по всей оси значений случайной величины равнялся единице. Вообще говоря ФР может принимать самые разнообразные очертания, но в огромном большинстве случаев ФР принимает вид " колокола". При этом вершина колокола является часто наиболее характерной точкой ФР. Определим следующую характеристику ФР: " центр распределения" Это наиболее характерная точка функции распределения визуально. Определений " центра распределения " может быть несколько. Рассмотрим три из них:

· мода- точка на оси Х соответствующая максимальному значению ФР. Такое определение даёт нам значение наиболее вероятного значения случайной величины. Но оно существует не для всякого распределения. Мод может быть не одно значение, если у ФР два или более максимума.

· медиана - точка на оси Х слева и справа от которой, суммы вероятностей событий равны по 0, 5.

· Математическое ожидание: определяется для дискретной величины формулой: Сумма Х(i)*р(I) по сути это среднее арифметическое значение всех возможных значений случайной величины. его можно обозначить как МО или как " мю".

Покажем, как МО необходимо для определения ожидаемой доходности при выплате дивидендов, поступлении купонных выплат. Пусть мы имеем от аналитика следующие данные: он определил, что на выплату дивидендов по акциям компании ZZZ будут влиять следующия события, вероятности которых и выплаты при этом будут соответствующими:

· снижение ключевой ставки на один процент, вероятность этого события он оценил величиной 0, 15 При этом дивиденды ориентировочно составят 79 р. р(к.с.) = 0, 15

·Невыдача кредита на развитие АО 0, 27 р(кредита)= 0, 27 Дивиденды составят в этом случае 40 р.

·Повышение в закупочных ценах вероятность р(цены вверх) = 0, 24 Дивиденды = 46

·Понижение закупочных цен р(цены вниз)= 0, 15 Дивиденды 57 р.

·Снижение цен на электроэнергию р(ЭЭ)= 0, 19: Дивиденды 51.

Требуется найти ожидаемую доходность:

Реализация одной из этих возможностей означает, что остальные варианты исключаются. Это называется взаимоисключающие события. Для суммы вероятностей именно таких наборов и существует требование, чтобы она была равна 1. Это я называю полным набором событий.

Ни одному из этих событий заранее не может быть сделано предпочтение, но именно одно из них реализуется.

Для вычисления на помощь приходит формула математического ожидания (МО).

Перемножим значения вероятностей на соответствующее значение дивидендов:

р(к.с)*0, 15+р(кредита)*40+р(цены вверх)*46+р(цены вниз) + р(ЭЭ)*51=0, 15*79+0, 27*40+0, 24*46+0, 15*57+0, 19*51= 51, 93. рублей. Это та сумма, которую может ожидать инвестор или " ожидаемая доходность". Так формула математического ожидания позволяет нам вычислять ожидаемую доходность инвестиций в акции ZZZ. Естественно, это можно проделать над многими ц.б. и пакетами. Надо только отметить, что это, достаточно искусственный пример, т.к. определить набор взаимоисключающих событий, не всегда просто.

Иногда, если для какого набора событий сумма вероятностей меньше единицы, можно добавить событие состоящее из нулевого значения случайной величины с недостающим значением вероятностей, доводящим общую сумму вероятностей до единицы.

Однако для наших целей наиболее важным является использование МО для вычисления двух более важных показателей: " дисперсия" и " стандартное отклонение" или " среднеквадратичное отклонение" Стандартное отклонение может быть обозначено как СО или буквой сигма, а дисперсия буквой Д или D.

Дисперсия вычисляется как сумма.................

СО = корень из дисперсии.

И тот и другой показатель интерпретируются, как степень неопределённости случайной величины и используются в равной степени в зависимости от удобства математических преобразований. Именно сигма характеризует предсказуемость инвестиций, да и других прогнозов. Никаких других показателей лучше сигмы и дисперсии подобрать не удалось за многие годы применения математической статистики.

Например, в нашем случае с дивидендами МО имело значение 51, 93 рубля. Найдём дисперсию и сигму.

Дисперсия составит 936, 84

Сигма = корень Д =30, 61

Таким образом, колебания величины дивидендов в нашем случае составит примерно 30 рублей.

Если, например сигма равна 0, то риск вложения в такую ц.б. равен или близок к 0. Как правило, это различные государственные ц.б..

Таким образом мы получили инструмент, с помощью которого мы можем оценить рискованность инвестиций в отдельно взятый финансовый инструмент, в нашем случае- ценную бумагу. Мы уже с вами обсуждали эффективность владения отдельно взятой ц.б. и понимаем, что ограничившись одной ц.б. мы не имеем никаких возможностей влиять на доходность такого владения. Разве что, мечась между всеми видами ц.б..

Важным и полезным инструментом исследования ц.б. является понятие " дерево событий".

Дерево событий подразумевает развитие процесса инвестирования в несколько этапов. Допустим в нашем инвестировании два этапа. Пусть мы предполагаем, например, что в следующем снабжение сырьём объекта инвестиций возможно от трёх взаимоисключающих поставщиков А, Б и В. Вероятность выбора А составляет 0, 26 выбор Б 0, 37 и В 0, 27. Напомним, сумма вероятностей равна 1. В свою очередь на следующий год возможны для каждого выбора три своих сценария. Ясно, что разыграется лишь один сценарий, но кроме того внутри любого из них кроются свои взаимоисключающие варианты. Пусть для поставщика А мы имеем вариант событий А1 с вероятностью р)А1)=0, 45 и дивидендами 10 руб., вариант А2 с вероятностью р(А2)= 0, 35 дивидендами 6 руб. и вариант А3 с вероятностью р(А3)=0, 2, с дивидендами 15 руб.

Аналогично, для поставщика Б (если он реализуется) имеем вариант Б1: с р(Б1)=0, 26 и дивиденды 3 р, ветка Б2: с р(Б2)= 0, 36 и дивидендами 10 руб. и ветка Б3: р(Б3)=0, 38 с дивидендами 15 руб.

Поставщик В ветка В1: р(В1)= 0, 2, дивиденды 13 руб. ветка В2: р(В2)= 0, 45 дивиденды 21 руб. и ветка В3: р(В3)=0, 35 дивиденды 18 руб. Перемножив попарно вероятность реализации первого варианта на вероятности его веток и на дивиденды и проделав тоже самое для Б и В, получим ожидаемые дивиденды в сумме 11, 04 рубля Вот, вкратце способ определения ожидаемой доходности владения ц.б. по дереву событий..

Лекция 6

Итак, мы с вами, подошли к созданию объекта управления. Поэтому мы с вами уже наметили, что наверное стоит попробовать владеть одновременно нескольким ценными бумагами в различной пропорции. Здравый смысл подсказывает нам, что это эффективнее, чем одна бумага. Но пока аппарата оценки у нас нет. Такой путь инвестирования мы называем созданием портфеля. А всё, что связано с определением состава ПОРТФЕЛЬсроков и других параметров, называем управлением портфелем. Соответственно, существует наука управления портфелем. Правда, мы ещё не сказали про параметры описывающие П. Сделаем же это. Во первых, такие характеристики как доходность и риск, как мы увидим в дальнейшем, присущи и ПОРТФЕЛЬ также как и ц.б..

Введём понятие состав ПОРТФЕЛЬ и понятие доля ценной бумаги.

Состав портфеля, это те ц.б. которые были куплены на сумму, выделенную для инвестирования. Вхождение в ПОРТФЕЛЬ для ц.б. характеризуется суммой денег, потраченных на их покупку. Т.о. у нас есть таблица, в которой отражены наименования ц.б. и суммы денег потраченных на их покупку. Неплохо дать в этой таблице количество и цену покупки ц.б.. Конечно, в таблице мы укажем ожидаемую доходность каждой ц.б., и её сигму (или дисперсию). Осталось понять, много или мало той или иной ц.б. по сравнению с другими, или в целом по отношению к размеру П. Такой показатель даётся долей ц.б. в составе. Доля ц.б. определяется как дробь вида Х(i)/(стоимость всех бумаг). Проделав эту операцию по всем бумагам, мы найдём все доли. По самому способу определения долей можно найти сумму долей. Она всегда равна единице. Этот факт иногда поможет нам упростить вычисления.

Теперь выпишем формулу для должности портфеля составленного из k бумаг, с заданными долями и ожидаемыми доходностями, определёнными тем или иным способом, в том числе и через ожидаемые альтернативы, как это показано в формуле для ОД.

Итак у наc есть сумма инвестиций или начальное благосостояние в размере Z0. Z0 вложено в k бумаг, сумма вложений в каждую ц.б. составляет S(i), а доходность i ц. бумаги задана как r(i), где индекс i пробегает значения от 1 до k. Обозначим конечное благосостояние инвестора через Zend. Тогда доход на весь портфель составит:

Доход на портфель: Z0*(1+R) = S(1)*(1+r(1))+S(2)*(1+r(2))+... +S(k)*(1+r(k))

Разделим обе части равенства на Z0 т.е. на общую сумму первичных инвестиции в портфель:

В левой части получим доходность портфеля в целом, а в правой, члены равенства вида X(i)*(1+r(i)) где X(i) есть выражение вида: S(i)/Z0 т.е. доля i бумаги в портфеле

В итоге получим ожидаемую доходность портфеля в виде

Проблема выбора портфеля.

Пусть мы имеем два портфеля А и Б

Портфель А Портфель Б

Начальное благосостояние 100 000 100 000

Конечное благосостояние Вероятности неполучения для А Вероятности неполучения для Б неполучения для Б

70 000 0 2

80 000 0 5

90 000 4 14

100 000 21 27

110 000 57 45

120 000 88 66

130 000 99 82

сигма 10 20

ожидаемая доходность 8 12

Как мы видим, выбор непрост т.к. Хотя П Б показал лучшую доходность Б имеет большую сигма, а портфель А имеет маленькую сигму, но и меньшую доходность. При этом ПОРТФЕЛЬ А лучше защищён от самых больших убытков и т.д..

Трудность возникает от того, что в нашем рассмотрении отсутствует ещё один фактор: отношение инвестора к риску и доходности.

Метод с который будет применён для выбора портфеля называется метод кривых безразличия.

Назовём пространством портфелей плоскость ((r, Ϭ) на которой по оси Х отложен риск портфеля, а по оси Y его доходность.

Наметим на плоскости точку с парой (r, Ϭ) и обратимся к нашему инвестору, говоря: вот сочетание доходность /риск. Выберем из окружающих точек, такую которую инвестор сочтёт эквивалентной соседней, потом ещё и ещё. Наметив достаточное количество точек, соединим их непрерывной линией. Все эти точки объединены одним параметром: безразличием инвестора к тому, в какой точке этой линии он бы выбрал портфель: все портфели на этой линии для него являются одинаково хорошими, эквивалентными: переходя от точки к точке он, теряя в доходности, увеличивает уверенность и одно точно компенсирует другое в его понимании. Такая линия называется: кривая безразличия. Поднявшись немного вверх и влево, поставим ещё одну стартовую точку и от неё построим ещё одну, смещённую вверх и влево. Действуя так ещё несколько раз, построим семейство кривых безразличия. Такое семейство характерно только для конкретного инвестора, который отвечал на наши вопросы. Другой инвестор, скорее всего, будет выбирать другие точки и семейство линий будет иметь другой наклон.

Проведём через наше семейство горизонтальную линию, линию равной доходности. Очевидно, что при придерживаясь равной доходности инвестор предпочёл бы оказаться как можно левее, если это возможно. Проведём теперь через семейство вертикальную линию, линию равного риска. Также очевидно, что при фиксированном риске инвестор предпочтёт двигаться вверх по этой вертикали. Объединив эти две тенденции, констатируем, что при выборе желаемого портфеля, инвестор склонен выбирать точки на пространстве, описывающие портфели, которые находятся выше и левее, насколько это возможно.

Концепция кривых безразличия позволяет нам определить, каким типам инвесторов свойственны семейства кривых безразличия. Оказывается, их можно разбить на три больших класса, отнесённых к консервативным инвесторам, сбалансированным и рискованным. Важным свойствами кривых безразличия является то, что они не пересекаются для одного типа инвесторов. Т.е. они как бы параллельны друг к другу. Вторым свойством является то, что их бесконечно много и они могут располагаться бесконечно близко друг к другу.

Кривые безразличия для Кривые безразличия для Кривые безразличия для

острожного инвестора рискового инвестора умеренного инвестора

Чтобы перейти к следующим темам, нам необходимо научиться рассчитывать качество портфеля. Качество ПОРТФЕЛЯ это его доходность и риск. Какие исходные данные мы имеем? Поскольку мы говорим о портфеле, мы имеем набор ценных бумаг. Вхождение ц.б. в портфель характеризуется тремя параметрами: её доходностью, долей в портфеле, и уровнем риска присущего этой ц.б. т.е. Ϭ

Мы уже знаем, как определить доходность портфеля, если известны доли ц.б. и доходность.

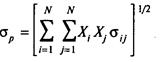Запишем формулу для вычисления Ϭ портфеля, известную из математической статистики:

(5.1)

В этой формуле переменная σ _{i, j} означает ковариацию двух случайных величин, в нашем случае- доходностей ценных бумаг. Двойное суммирование в формуле означает, что при каждом фиксированном значении i j пробегает от 1 до N. Затем i принимает следующее по порядку значение и суммирование по j повторяется. Т.о. количество полной? развёрнутой цепочки членов суммы будет равно N в квадрате, в том числе члены, в которых i = j. Ковариация, это статистическая мера величины взаимозависимости двух случайных величин. Если в наборе имеется n компонентов, то таких ковариаций будет n², включая и самоковариации, т.е. ковариации ц.б. с самими собой, а полное описание все ковариаций будет представлять из себя квадратную матрицу, симметричную относительно главной диагонали. Т.о., если в портфеле, например три ц.б., то членов суммирования будет 9, три из которых будут с совпадающими индексами, что говорит о том, что это члены, которые характеризуют чистый, независимый вклад каждой из трёх бумаг в Ϭ портфеля. Отметим, что диапазон значений ковариации ничем не ограничен в связи с чем, не всегда понятно, насколько велико влияние ц.б. друг на друга. Мы знаем только, что положительные значения говорят о движении доходности в одном направлении, а отрицательные значения- о противоположном направлении. Если ковариация равна нулю, это говорит о полной независимости доходностей ц.б. В этом случае набор точек, на которых определяют ковариацию, выглядит как бесформенное облачко точек. Чтобы точнее определить силу взаимозависимости удобнее применить другой показатель- коэффициент корреляции. Это нормированный показатель и его значение заключено в пределах от -1 до +1. Величина корреляции +1 означает полное согласование двух доходностей, т.е. если одна из доходностей измениться на 25% то вторая увеличится ровно также. Соответственно чем ближе ρ к нулю тем менее зависимы доходности. При ρ равном 0 налицо полная независимость. отрицательные значения это антизависимость при ρ равном -1, доходности меняются в противоположных направлениях. ρ удобнее во многих смыслах. Однако с точки зрения вычислительной иногда бывает удобнее применять и ковариацию. Ковариация и корреляция связаны соотношением.

Рассмотрим, как выглядит ф(5.1) для трёх ц.б., входящих а портфель:

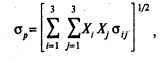
Или

Пусть доля акций вида А равна 0, 235, доля акций вида Б равна 0, 407, а доля акций вида В равна 0, 3605

Ковариационная матрица задана такими значениями:

146 187 145

187 854 104

145 104 289

Отметьте симметрию матрицы. Элементы: а(2, 1) = а(1, 2), а(1, 3) =а(3, 1), а(2, 3) =а(3, 2). Диагональные элементы равны Ϭ в квадрате акциям 1, 2 и 3 вида, т.е. дисперсии акций.

Вычислив Ϭ портфеля по этим данным, получим 16, 65%

Перейдём к выбору портфеля.

Если мы возьмём для исследования портфель из двух ценных бумаг: бумагу А с доходностью 5% и Ϭ 20% и бумагу Б с доходностью 15% и Ϭ 40% и построим все возможные портфели из них на плоскости (r, Ϭ) то обнаружим, что они выстраиваются в фигуру изображённую на рис ниже:

Точка Б соответствует случаю, когда в портфеле только бумага Б, точка А содержит в портфеле только бумагу А. Если мы построим достаточное количество точек, соответствующих разным долям бумаг А и Б в портфеле, то получим кривую соединяющую эти точки. На ней располагаются все возможные портфели из бумаг А и Б.

Кривая, которую мы получили, есть простейший случай достижимого множества портфелей для двух ц.б..

В более общем случае, если в нашем распоряжении на рынке имеется некоторое множество самых различных ценных бумаг, да и других инструментов инвестирования, подобное множество портфелей называется достижимое множество: достижимое множество содержит все возможные портфели для данного набора ценных бумаг. В общем случае оно выглядит так:

.

Основываясь на свойстве наилучших портфелей устремляться вверх и налево обнаружим, что самые эффективные портфели располагаются на левой границе нашего эффективного множества между точками S и Е. При этом портфели ниже и правее точки Е будут уже не лучшими. Так мы выделяем из нашего достижимого множества " эффективное множество". Это ключевое понятие теории. Осталось только совместить описанные ранее кривые безразличия с эффективным множеством. Вот как это выглядит на плоскости (r, Ϭ):

Становится ясно, что одна из кривых семейство кривых безразличия, свойственных тому или иному уровню риска, " соприкасаются с эффективным множеством в одной единственной точке. Всё что внутри достижимого множества не самое эффективное, а всё, что выше эффективного множества- не существует. Ведь мы нашли все и только достижимые портфели.

Для построения эффективного множества существует специальный математический аппарат- " алгоритм квадратического программирования" или " метод критических линий". Здесь мы его рассматривать не будем.