Рыночная модель

Пусть доходность акции за некий период (пусть это месяц или 6 месяцев), связана с доходностью на рыночный индекс, например индекс ММВБ. Такой путь носит название рыночная модель

Вид такой зависимости может быть такой:

Где:

r_i доходность i бумаги за выбранный период.

R _I доходность на индекс за тот же период

α _{i, I}: коэффициент смещения

β _{i, I} коэффициент наклона(связи r _i и r_I)

ε _{i, I} случайная погрешность

α β ρ ε Ϭ

В таком виде уравнение рыночной модели описывает, насколько доходность на ц.б. связана с доходностью на индекс. Как мы увидим, такой подход позволяет разделить риски, связанные с общим движением рынка т.н. систематический, рыночный риск и риск присущий только выбранной в данный момент бумагой. Не надо забывать, что все единицы по осям здесь проценты.

Пусть: α _{i, I} =4%, β _{i, I} =1, 2 R _I

Запишем получившееся уравнение:

r_i = 4+ 1, 2 R _I + ε _{i, I}

Если пренебречь случайной погрешностью, получим следующий график:

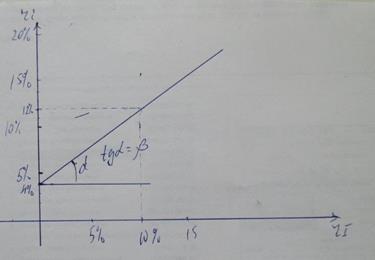
Здесь коэффициент смещения показывает, какую доходность будет иметь ценная бумага, если доходность рынка будет равна 0. Этот коэффициент может быть и отрицательным. Важно отметить значение β _{i, I}: его величина для любой данной бумаги характеризует её.Этот коэфф. показывает чувствительность ценной бумаги к изменениям рынка. Если β _{i, I} < 1 то такая ц.б. является консервативной, «оборонительной», если β _{i, I} > 1 то такая ц.б. называется агрессивной, ну а β _{i, I} =1- нечто среднее умеренное. Заметьте, пока мы говорим только о отдельной бумаге.

Вычисление β _{i, I} проводится по следующей формуле из математической статистики:

β _{i, I} = σ _{i, I}/ σ _I ²,

где:

σ _{i, I} - ковариация между доходностью ценной бумагой и доходностью на индекс

σ _I² - дисперсия доходности индекса

Диверсификация

Дальнейшие наши рассуждения будут направлены на разделение двух составляющих риска для ценной бумаги. Риск для ценной бумаги можно записать в следующем виде.

σ _{i, I}² = β _{i, I} ² σ _I ² + Ϭ _{i, I} ² α β ρ ε Ϭ

Хотя здесь Ϭ во второй степени, это нас не смущает, просто это удобнее для вычислений, мы всегда можем извлечь корень квадратный.

Теперь перейдём к параметрам портфеля. Нам известна формула вычисления доходности портфеля, если даны доходности и доли ценных бумаг:

r _p = Σ (X_{i *} r_i), выражение

Где суммирование идёт по всем бумагам портфеля

Подставим выражение для R _p в уравнение рыночной модели

получим:

где:

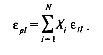
К нашему удовольствию мы видим, что α, β, ε являются средневзвешенными соответствующих коэффициентов входящих в портфель.

Это позволяет нам применить все выводы относящиеся к портфелю, как и к отдельной ц.б.

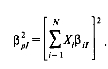Тогда и общий риск для портфеля выглядит так:

где

β _pI² носит название рыночный риск портфеля, σ _{ε , p}² является собственным риском портфеля.

Рассмотрим рыночный риск- β _pI²

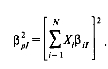
Если принять, что доли входящих бумаг примерно равны и малы, т.к. их может быть достаточно много, то мы можем вынести за знак суммирования коэффициент 1/N и получим:

- β _pI² = 1/N Σ β _pI² это означает, что коэффициенты β _pI² усредняются по портфелю и никакая ценная бумага не окажет на риск портфеля существенного влияния. Влияние будет лишь в той степени, в которой будет высока или низка доходность на индекс, т.е. общее состояние рынка. Этот риск неустраним за счёт подбора бумаг. Это и есть рыночный риск.

Обратимся теперь ко второму слагаемому, он носит название несистематический риск или собственный риск портфеля.

Считая, что в среднем

Доли каждой бумаг

Равны 1/N получим:

Вынесем 1/N за сумму:

Тогда выражение:

Будет равно среднему

σ _{ε , p}² по портфелю

А собственный риск

Портфеля уменьшится

N Раз.

Или, если мы перейдём к корню из дисперсии, то σ _{ε , p} уменьшится в N степени ½.

Именно этот эффект и необходимо было получить.