
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
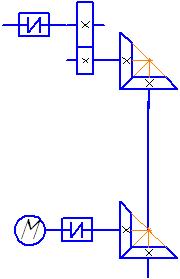
Кинематические схемы привода
|
|
1. 
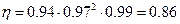
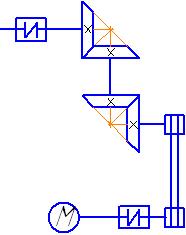
2. 
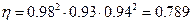
3.

1. Определение мощностей и передаваемых крутящих моментов,  расчёты передач, соединений и валов.
расчёты передач, соединений и валов.
1. 1 КПД привода
η =η р·η к2·η п3=0, 94·0, 972·0, 9942=0, 86
1.2 Мощность
Рр =Рвых/η общ=2.75/0, 86=3, 19 КВт
Частота вращения выходного вала
n вых=30ω /π =30·12/3, 14=114, 6 мин-1
Передаточное число привода
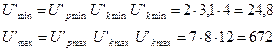
1.5 Расчетная частота вращения вала электродвигателя
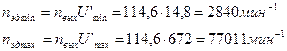
1.6 Выбираем электродвигатель
Р эд > Р р и 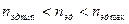
Выбираем двигатель 4А90L2У3 с параметрами
Р эд = 3 кВт - перегрузка не превышает 5%.
nэд = 2880 мин-1
Tпуск/Tн=2, 0
М= 25 кг
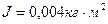
1.7 Действительное общее передаточное число привода
U0 = n эд / n вых =2880/114, 6 = 24, 78
1.8 Действительные передаточные числа передач привода выбираем так чтобы U0=UрUкUк
Uр=2 Uк з=3 Uк о=4, 13
U0=2·3·4, 13=24, 78
1.9 Силовые и кинематические параметры валов привода
1.10 Мощности на валах:
Р= Рр=3, 19 КВт
Р1= Р· η р · η п=3, 19·0, 94·0, 994=2, 98 КВт
Р2= Р1· η к · η п=2, 98·0, 97·0, 994=2, 87 КВт
Р3= Р2· η к · η п=2, 87·0, 97·0, 994=2, 75 КВт
1.11 Частоты вращения валов:
n = n эд = 2880 мин-1
n1 = n / Uр =2840/2=1420 мин-1
n2 = n1 / Ur =1425/3, 0=473, 33 мин-1
n3 = n2 / Ur =473, 33/4, 13=114, 6 мин-1
1.12 Передаваемые крутящие моменты:
Т=Тэд=9550·(Р эд /n эд )=9550·(3, 19 /2840)= 10, 5 Нм
Т1=9550·(Р 1 /n 1 )=9550·(2, 98 /1420)= 19, 7 Нм
Т2=9550·(Р 2 /n 2 )=9550·(2, 87 /473, 33)= 57, 1 Нм
Т3=9550·(Р 3 /n 3 )=9550·(2, 75 /114, 6)= 230, 5 Нм
1.13 Определяем диаметры валов привода из расчёта только на кручение при пониженных допускаемых напряжениях
d = 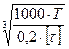 =
=  =12 мм
=12 мм
d 1 = 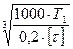 =
= 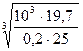 =15 мм
=15 мм
d 2 = 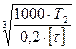 =
= 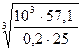 =22 мм
=22 мм
d 3 = 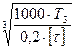 =
= 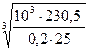 =35 мм
=35 мм
2. Расчёт клиноременной передачи
Исходные данные:
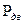 =3, 19 КВт
=3, 19 КВт
n=2840 мин-1
а=1100 мм
2.1 Сечение ремня
2.2 Из таблицы сечение ремней выбираем О.
Принимаем диаметр меньшего шкива для, для О d 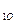 =63 мм.
=63 мм.
Окончательно принимаем d 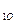 =63 мм.
=63 мм.
Размеры сечений ремней следующие
О: В 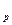 =8, 5 мм, В=10 мм, Н
=8, 5 мм, В=10 мм, Н 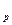 =6 мм, Н=2, 1 мм
=6 мм, Н=2, 1 мм
2.3 Расчётный диаметр ведомого шкива
О: d 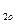 =d
=d 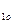 ∙ u= 63∙ 2=126 мм
∙ u= 63∙ 2=126 мм
Окончательно принимаем
d 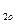 =125 мм
=125 мм
2.4 Действительное передаточное число проектируемой передачи
U 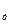 =
= 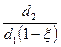
 - коэффициент упругого скольжения
- коэффициент упругого скольжения
O: U 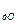 =
= 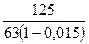 = 2
= 2
2.5 Минимальное межосевое расстояние
а 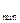 =0, 55
=0, 55  +Н
+Н 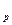 ;
;
О: а 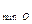 =0, 55
=0, 55 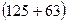 +6=109, 4 мм;
+6=109, 4 мм;
O: а 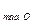 =2
=2 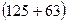 =376 мм;
=376 мм;
Принимаем среднее значение межосевого расстояния а=280мм;
2.6 Расчётная длина ремня
L 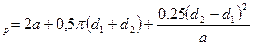
O: L’ 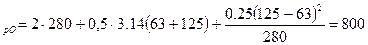 мм
мм
Расчётную длину для ремня О принимаем ближайшую к вычисленной L=800, так как расхождение стандартной и вычисленной не превышает 5%.
Определяем остальные параметры для сечения О.
2.7 Коэффициент учитывающий длину ремня
С 
2.8 Угол обхвата ремнём меньшего шкива

Определяем коэффициент С 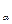 , учитывающего влияние угла обхвата на ведущем шкиве по формуле
, учитывающего влияние угла обхвата на ведущем шкиве по формуле
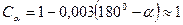
2.9 Определяем скорость ремня
 м/с
м/с
2.10 число ремней передачи.
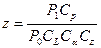
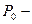 мощность передаваемая одним ремнём
мощность передаваемая одним ремнём
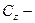 коэффициент, учитывающий число ремней в передаче
коэффициент, учитывающий число ремней в передаче
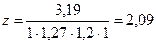
Принимаем z=2
2.11 Сила нагружающая валы передачи
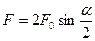
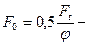 предварительное натяжение ремня
предварительное натяжение ремня
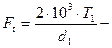 окружное усилие
окружное усилие
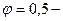 коэффициент тяги
коэффициент тяги
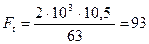 Н
Н
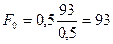 Н
Н
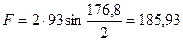 Н
Н
3. Расчёт цилиндрической косозубой закрытой передачи.
Материал и допускаемые напряжения.
Исходные данные:
 мин-1
мин-1
 мин-1
мин-1
U=3, 0
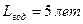
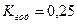
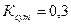
3.1 Из условия выбора материала для зубчатых колес HB1= HB2+20÷ 40. Материалы для зубчатых колёс принимаем 40Х (улучшение) со следующими механическими свойствами
Для шестерни: 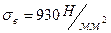 ,
,  , HB=280
, HB=280
Для колеса:  ,
, 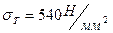 , HB=260
, HB=260
3.2 Допускаемые контактные напряжения. Так как проектируемая передача является открытой, то допускаемые контактные напряжения не определяются.
3.3 Базовое число циклов, соответствующее пределу выносливости для шестерни и зубчатого колеса определим по рис.4.1.3.(Атлас).
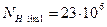
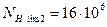
3.4 Эквивалентное число циклов
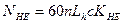
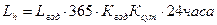
с= 1-число зацеплений зуба за 1 оборот (рис.4.1.5. Атлас).
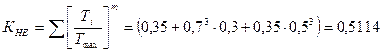
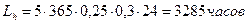
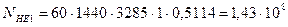 циклов
циклов
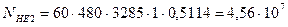 циклов
циклов
3.5 Коэффициент долговечности
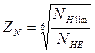
Так как 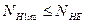 , то
, то 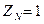
3.6 Предел контактной выносливости
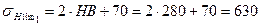 МПа
МПа
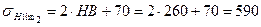 МПа
МПа
3.7 Допускаемые контактные напряжения

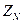 -коэффициент запаса прочности
-коэффициент запаса прочности
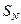 =1, 1-для зубчатых колёс с однородной структурой
=1, 1-для зубчатых колёс с однородной структурой
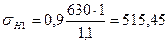 МПа
МПа
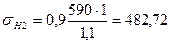 МПа
МПа
3.8 Расчёт допускаемого контактного напряжения
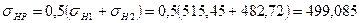 МПа
МПа
3.9 Допускаемые изгибные напряжения
3.10 Базовое число циклов напряжений
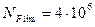 цикл
цикл
Эквивалентное число циклов


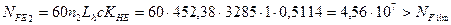
3.11 Предел выносливости зубьев при изгибе
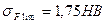
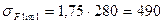 МПа
МПа
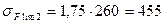 МПа
МПа
3.12 Допускаемые изгибные напряжения
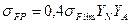
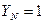 т.к.
т.к. 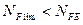
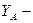 коэффициент учитывающий влияние двухстороннего приложения нагрузки
коэффициент учитывающий влияние двухстороннего приложения нагрузки
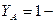 при одностороннем
при одностороннем
 МПа
МПа
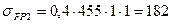 МПа
МПа
3.13 Допускаемые напряжения при действии максимальной нагрузки
3.14 Допускаемые контактные напряжения
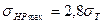
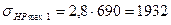 МПа
МПа
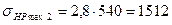 МПа
МПа
3.15 Допускаемые изгибные напряжения
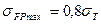
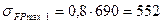 МПа
МПа
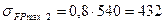 МПа
МПа
3.1 Прочностной расчёт.
3.1.1 Расчёт межосевого расстояния.
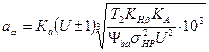
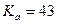 МПа
МПа 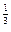
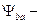 коэффициент ширины шестерни относительно межосевого расстояния
коэффициент ширины шестерни относительно межосевого расстояния
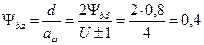
Принимаем 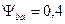
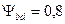
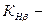 коэффициент, учитывающий неравномерность распределения нагрузки по ширине венца
коэффициент, учитывающий неравномерность распределения нагрузки по ширине венца
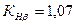
 коэффициент внешней динамической нагрузки
коэффициент внешней динамической нагрузки
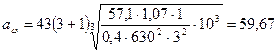 мм
мм
Берём 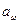 =63
=63
3.1.2 Ширина венцов, мм
Зубчатое колесо: b2 = ψ ba ·a = 0, 4·59, 67 = 23, 86 мм;
Принимаем b2=24 мм;
Шестерня: b1 = b2+2=24+2=26 мм;
3.1.3 Принимая  , определим модуль зацепления
, определим модуль зацепления
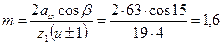
Принимаю, ближайший нормальный модуль mn = 1, 5 мм.
3.1.4 Суммарное число зубьев передачи
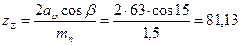
Принимаем 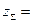 82
82
3.1.5 Действительный угол наклона зуба
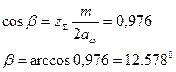
3.1.6 Число зубьев шестерни
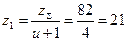
Число зубьев зубчатого колеса
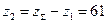
3.1.7 Действительное передаточное число

3.1.8 Диаметры зубчатых колёс, мм
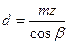
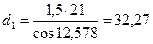 мм
мм
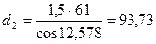 мм
мм
Диаметры вершин зубьев
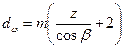
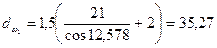 мм
мм
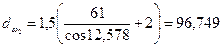 мм
мм
3.2 Проверочный расчёт на выносливость по контактным напряжениям.
3.2.1 Окружная сила в зацеплении, Н
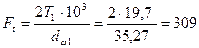 Н
Н
3.2.2 Окружная скорость колёс, м/с
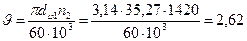 м/с
м/с
3.2.3 Выбираю степень точности передачи по нормам плавности (табл. 4.1.14 Атлас). 9 – ю степень точности для передачи.
3.2.4 Удельная окружная динамическая сила (см. (6.10) ч.1, [1]):
 Н/мм
Н/мм
δ H-коэффициент, учитывающий влияние вида зуба и модификации профиля на динамическую нагрузку. δ H = 0.002 (см. табл. 6.10 ч.1, [1]);
go- коэффициент, учитывающий влияние разности шагов зацепления зубьев шестерни и колеса. go = 73 (см. табл. 6.11 ч.1, [1]).
3.2.5 Удельная расчётная окружная сила в зоне её большей концентрации:
 Н/мм
Н/мм
3.2.6 Коэффициент, учитывающий динамическую нагрузку, возникающий в зацеплении (см. (6.9) ч.1):
КHV= 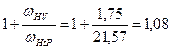
3.2.7 Удельная расчетная окружная сила ω Ht, Н/мм (см. (6.8) ч.1):
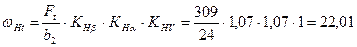 Н/мм
Н/мм
3.2.8 Расчетные контактные напряжения (см. (6.7) ч.1, [1]):

где zH = 1, 77cos  = 1.72575.
= 1.72575.
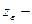 коэффициент, учитывающий суммарную длину контактных линий
коэффициент, учитывающий суммарную длину контактных линий
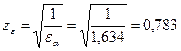
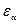 - коэффициент торцевого перекрытия
- коэффициент торцевого перекрытия
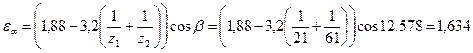
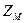 - коэффициент, учитывающий механические свойства материала колёс.
- коэффициент, учитывающий механические свойства материала колёс. 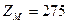 МПа.
МПа.
3.3 Проверка расчётных напряжений.
3.3.1 Определяю удельную окружающую динамическую силу:
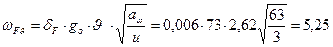 Н/мм
Н/мм
3.3.2 Удельная расчётная окружная сила в зоне её большей концентрации:
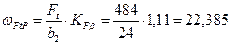 Н/мм
Н/мм
3.3.3 Коэффициент, учитывающий динамическую нагрузку, возникающий в зацеплении (см. (6.9) ч.1):
КFV= 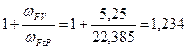
3.3.4 Удельная расчетная окружная сила ω Ft, Н/мм:
 Н/мм
Н/мм
3.3.5 Коэффициент, учитывающий форму зуба



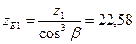

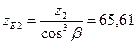
По графику 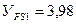
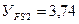
Определяю отношения σ FP/ YF при σ FP = 196 МПа для шестерни и σ FP = 182 МПа для колеса:
шестерни колеса
σ FP/ YF =196/3, 98 = 49, 25; σ FP/YF =182 /3, 74=48, 66
Таким образом, расчеты следует вести по колесу z2 (6.6.3 ч.1, [1]).
3.3.6 Расчётные напряжения изгиба зуба

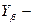 коэффициент, учитывающий наклон зуба
коэффициент, учитывающий наклон зуба

 - коэффициент, учитывающий перекрытие зубьев
- коэффициент, учитывающий перекрытие зубьев
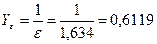
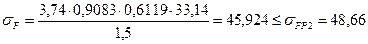 МПа
МПа
3.4 Проверка прочности зубьев при перегрузках.
3.4.1 Максимальные контактные напряжения
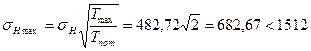 МПа
МПа
3.4.2 Максимальные напряжения изгиба
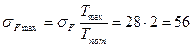 МПа
МПа
3.5. Силы в зацеплении.
3.5.1 Окружные силы
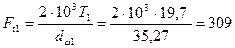 Н
Н
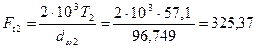 Н
Н
3.5.2 Радиальные силы
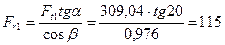 Н
Н
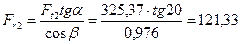 Н
Н
3.5.3 Осевые силы
 Н
Н
4. Расчёт цилиндрической прямозубой закрытой передачи.
Материал и допускаемые напряжения.
Исходные данные:
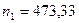 мин-1
мин-1
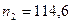 мин-1
мин-1
U=4, 13
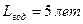
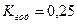
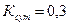
4.1 Материалы для зубчатых колёс принимаем 40Х (улучшение) со следующими механическими свойствами
Для шестерни: 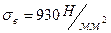 ,
,  , HB=280
, HB=280
Для колеса:  ,
, 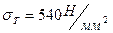 , HB=260
, HB=260
4.2Допускаемые контактные напряжения
4.3 Базовое число циклов, соответствующее пределу выносливости для шестерни и зубчатого колеса

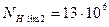
4.4 Эквивалентное число циклов
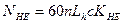
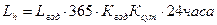
с= 1-число зацеплений зуба за 1 оборот
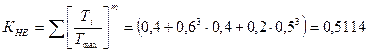
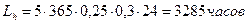
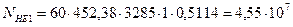 циклов
циклов
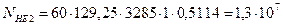 циклов
циклов
4.5 Коэффициент долговечности
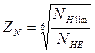
Так как 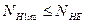 , то
, то 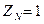
4.6 Предел контактной выносливости
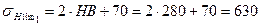 МПа
МПа
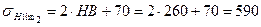 МПа
МПа
4.7 Допускаемые контактные напряжения

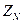 -коэффициент запаса прочности
-коэффициент запаса прочности
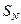 =1, 1-для зубчатых колёс с однородной структурой
=1, 1-для зубчатых колёс с однородной структурой
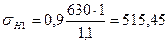 МПа
МПа
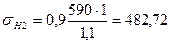 МПа
МПа
4.8 Расчёт допускаемого контактного напряжения
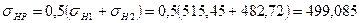 МПа
МПа
4.9Допускаемые изгибные напряжения
4.10 Базовое число циклов напряжений
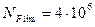 цикл
цикл
Эквивалентное число циклов

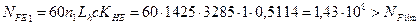
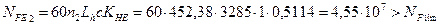
4.11 Предел выносливости зубьев при изгибе
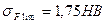
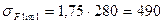 МПа
МПа
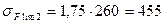 МПа
МПа
4.12 Допускаемые изгибные напряжения
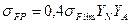
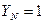 т.к.
т.к. 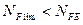
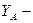 коэффициент учитывающий влияние двухстороннего приложения нагрузки
коэффициент учитывающий влияние двухстороннего приложения нагрузки
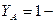 при одностороннем
при одностороннем
 МПа
МПа
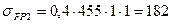 МПа
МПа
4.13 Допускаемые напряжения при действии максимальной нагрузки
4.14 Допускаемые контактные напряжения
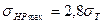
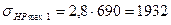 МПа
МПа
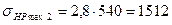 МПа
МПа
4.15 Допускаемые изгибные напряжения
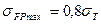
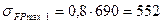 МПа
МПа
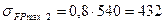 МПа
МПа
4.17 Расчетное межосевое расстояние, мм
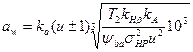
где 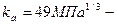 для прямозубых передач;
для прямозубых передач;
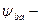 коэффициент ширины шестерни относительно межосевого расстояния =0, 35
коэффициент ширины шестерни относительно межосевого расстояния =0, 35  ,
,
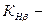 коэффициент, учитывающий неравномерность распределения нагрузки по ширине венца
коэффициент, учитывающий неравномерность распределения нагрузки по ширине венца
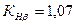
 коэффициент внешней динамической нагрузки
коэффициент внешней динамической нагрузки
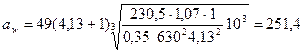 мм
мм
Величину 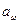 округляем до ближайшего значения в соответствии с ГОСТ 2185-86
округляем до ближайшего значения в соответствии с ГОСТ 2185-86
Примем 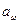 =250 для того что бы избежать затем перерезание колесами валов при компоновке редуктора.
=250 для того что бы избежать затем перерезание колесами валов при компоновке редуктора.
4.18 Ширина венца зубчатого колеса
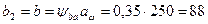 мм
мм
4.19 Ширина венца шестерни
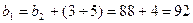 мм
мм
4.20 Прямозубые передачи
4.21 Принимая предварительно 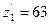
 , определяют модуль зацепления
, определяют модуль зацепления
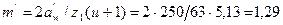
4.22 Число зубьев шестерни 

4.23 Число зубьев колеса 
4.24 Действительное передаточное число
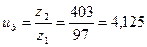
4.25 Диаметры зубчатых колёс, мм
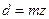
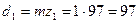 мм
мм
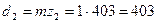 мм
мм
4.26 Диаметры вершин зубьев
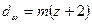
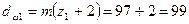 мм
мм
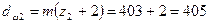 мм
мм
4.1 Проверочный расчёт на выносливость по контактнымнапряжениям.
4.1.1 Окружная сила в зацеплении, Н
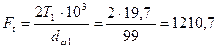 Н
Н
4.1.2 Окружная скорость колёс, м/с
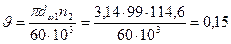 м/с
м/с
4.1.3 Выбираю степень точности передачи по нормам плавности 9 – ю степень точности для передачи.
4.1.4 Удельная расчетная окружная сила ω Ht, Н/мм (см. (6.8) ч.1):
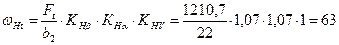 Н/мм
Н/мм
4.1.5 Расчетные контактные напряжения (см. (6.7) ч.1, [1]):

где zH = 1, 77.
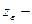 коэффициент, учитывающий суммарную длину контактных линий
коэффициент, учитывающий суммарную длину контактных линий
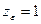
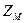 - коэффициент, учитывающий механические свойства материала колёс.
- коэффициент, учитывающий механические свойства материала колёс. 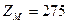 МПа.
МПа.
4.2 Проверка расчётных напряжений.
4.2.1.Удельная расчетная окружная сила ω Ft, Н/мм:
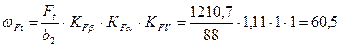 Н/мм
Н/мм
Коэффициент, учитывающий форму зуба
По графику 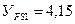
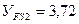
Определяю отношения σ FP/ YF при σ FP = 552 МПа для шестерни и σ FP = 432 МПа для колеса:
шестерни колеса
σ FP/ YF =552/4, 15 = 133; σ FP/YF =432 /3, 72=116, 12
Таким образом, расчеты следует вести по колесу z2 .
4.2.5 Расчётные напряжения изгиба зуба

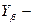 коэффициент, учитывающий наклон зуба
коэффициент, учитывающий наклон зуба
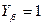
 - коэффициент, учитывающий перекрытие зубьев
- коэффициент, учитывающий перекрытие зубьев
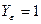
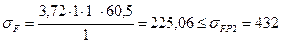
4.3 Проверка прочности зубьев при перегрузках.
4.3.1 Максимальные контактные напряжения
 МПа
МПа
4.3.2 Максимальные напряжения изгиба
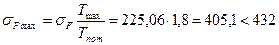 МПа
МПа