Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Действия над матрицами.
|
|
1. Сложение матриц - поэлементная операция
Суммой матриц A=(ay), B=(by) одинаковой размерности mxn называется матрица C= (aij+bij), i=1, m j=1, n.
2.Умножение матриц на число.
Произведением матрицы А на число µ называется матрица B= µA= (µA), i=1, m j=1, n.
3. Умножение матриц.
Произведением матрицы А=(аij) размерности mxn на матрицу B=(bij) размерности pxn (число столбцов матрицы А должно быть равно числу строк матрицы В) называется матрица C= (a1j+b1j+ ai2+b2j+…+ aip+bpj), i=1, m j=1, n.
3) Обра́ тная ма́ трица — такая матрица A− 1, при умножении на которую исходная матрица A даёт в результате единичную матрицу E:
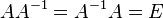
Свойства обратной матрицы[править | править вики-текст]
· 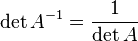 , где
, где  обозначает определитель.
обозначает определитель.
·  для любых двух обратимых матриц
для любых двух обратимых матриц  и
и  .
.
· 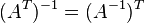 , где
, где  обозначает транспонированную матрицу.
обозначает транспонированную матрицу.
·  для любого коэффициента
для любого коэффициента  .
.
·  .
.
· Если необходимо решить систему линейных уравнений 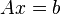 , (b — ненулевой вектор) где
, (b — ненулевой вектор) где  — искомый вектор, и если
— искомый вектор, и если  существует, то
существует, то  . В противном случае либо размерность пространства решений больше нуля, либо их нет вовсе.
. В противном случае либо размерность пространства решений больше нуля, либо их нет вовсе.
4) Система линейных алгебраических уравнений (линейная система, также употребляются аббревиатуры СЛАУ, СЛУ) — система уравнений, каждое уравнение в котором является линейным — алгебраическим уравнением первой степени.
Общий вид системы линейных алгебраических уравнений: