Нормой вектора евклидова пространства называется арифметический квадратный корень из скалярного вектора.

23) Вектора a и b называются ортогональными, если угол между ними равен 90°. (рис. 1). Условие ортогональности векторов. Два вектора a и b ортогональны (перпендикулярны), если их скалярное произведение равно нулю.

24) Ортогональный (ортонормированный) базис — ортогональная (ортонормированная) система элементов линейного пространства со скалярным произведением, обладающая свойством полноты.

24) Процесс Грама ― Шмидта ― наиболее известный алгоритм ортогонализации, при котором по линейно независимой системе 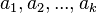строится ортогональная система такая, что каждый вектор линейно выражается через , то есть матрица перехода от к ― верхнетреугольная матрица. При этом можно добиться того, чтобы система была ортонормированной и чтобы диагональные элементы матрицы перехода были положительны; этими условиями система и матрица перехода определяются однозначно.

25) Симметричной (Симметрической) называют квадратную матрицу, элементы которой симметричны относительно главной диагонали.

ненулевой вектор 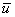, который при умножении на некоторую квадратную матрицу превращается в самого же себя с числовым коэффициентом 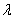, называется собственным вектором матрицы . Число 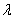называют собственным значением или собственным числом данной матрицы.

25) На плоскости дано конечное число точек, причем такое, что любая прямая, проходящаячерез две из данных точек, содержит еще одну данную точку. Тогда все данные точки лежатна одной прямой.{\displaystyle a_{11}x^{2}+a_{22}y^{2}+a_{33}z^{2}+2a_{12}xy+2a_{23}yz+2a_{13}xz+2a_{14}x+2a_{24}y+2a_{34}z+a_{44}=0}