
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Теоритические аспекты метода АСФ.
|
|
Основная идея непараметрической модели DEA [Charnes et al., 1978] заключается в представлении эффективности университета (в общем случае любой фирмы, производящей какой либо продукт) в виде отношения его результатов (выходных параметров) к потраченным ресурсам (входным параметрам). Рассмотрим задачу дробно-линейного программирования:

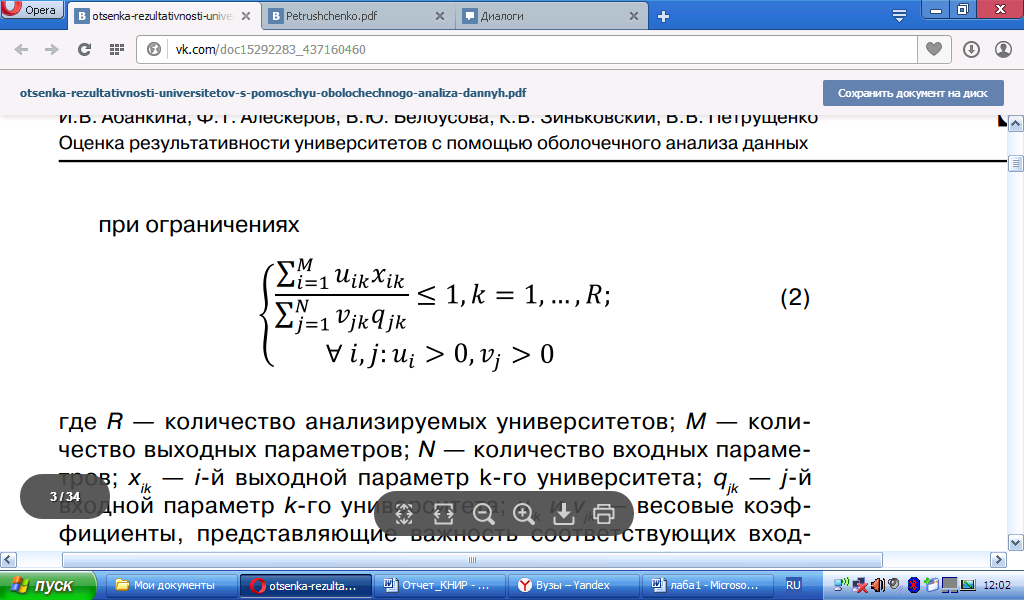
где R – количество анализируемых университетов;
M – количество выходных параметров;
N – количество входных параметров;
xik — i-й выходной параметр k-го университета;
qjk – j-й входной параметр k-го университета;
uik и vjk – весовые коэффициенты, представляющие важность соответствующих входных или выходных параметров. Здесь ek обозначает эффективность k-го университета.
Задача (1) представляет собой формулировку модели DEA. Основное преимущество данной модели заключается в автоматическом выборе весовых коэффициентов и для каждого входного и выходного параметра согласно критерию (1).
Кроме того, задача дробно-линейного программирования (1) с ограничениями (2) может быть приведена к задаче линейного программирования с помощью преобразования, предложенного А.Чарнзом и В. Купером:

где θ k – скаляр, представляющий эффективность k-го университета;
λ – R× 1 вектор констант;
Q – M× R матрица выходных параметров всех университетов;
X – N× R матрица входных переменных.
В данной формулировке константа θ k лежит в отрезке [0, 1], причем значение θ k = 1 указывает на 100% эффективность k-го университета относительно данной выборки и выбранных параметров входа и выхода.
Модель (3) с ограничениями (4) носит название модели DEA с постоянной отдачей от масштаба (Constant Return to Scale, CRS). Применение такой модели DEA оправданно в том случае, когда все анализируемые университеты оперируют в оптимальном для них объеме выпуска. В результате решения одной из двойственных задач (см. формулы (1)–(2) или (3)–(4)) находится оптимальный коэффициент результативности для каждого вуза. Этот балл рассчитывается путем повторения описанной выше процедуры индивидуально для каждого учебного заведения относительно тех, которые находятся в выборке. Значение этого показателя меньше или равно 1.
В первом случае вуз считается менее эффективным по сравнению с другими, во втором максимально результативным относительно исследуемой выборки.
Построение границ эффективности по методу DEA позволяет получить представление об относительном положении вуза, которое характеризует его ключевую деятельность в многомерном пространстве входных и выходных параметров на основе расчета эталонов эффективности по исходной выборке и определения относительной результативности каждого вуза, включенного в выборку. В случае модели (1–2) в качестве границы эффективности будет выступать кривая производственных возможностей, для модели (3–4) изокванта (кривая фиксированного объема производства при прочих равных).
Графическая иллюстрация метода DEA по модели (3–4) для случая, когда объекты характеризуются двумя входными параметрами и одним выходным и в качестве границы эффективности анализируется изокванта, представлена на рисунке 1, где x1, x2 — входные параметры, q — выходной параметр.

Рисунок 1 – Граница эффективности при задаче DEA по минимизации ресурсов вузов
Из рисунка 1 видно, что множество эталонных вузов (эффективных по выборке) состоит из учебных заведений под номерами 2 и 5. Их комбинация определяет оболочечную поверхность 3, или границу 3., относительно которой оценивается эффективность 1-го, 3-го и 4-го учебных заведений. Эффективность, например, вуза под номером 4 рассчитывается как отношение отрезка 04 к отрезку 04. Для этого университета ближайшими эффективными вузами будут 2 и 5, именно их относят к группе эталонов (peers) для этих неэффективных университетов. В свою очередь, 1, 3, 4 являются проекциями неэффективных вузов на границу эффективности. Соответствующие для них значения x1, x2 и q представляют собой эффективные цели (targets) для низкорезультативных вузов, т.е. значения входных и выходных переменных, которые для них по данной выборке считаются оптимальными.
Кроме модели (3) отдельно принято выделять версию DEA с учетом эффекта масштаба. Ее отличие заключается в добавлении еще одного ограничения к (4):
1Tl=1
Эта версия модели (3), с ограничениями (4)–(5) носит название модели DEA с переменной отдачей от масштаба (Variable Return to Scale, VRS). Ограничение гарантирует сравнение неэффективных университетов только с вузами приблизительно такого же размера, что не обязательно в модели с постоянной отдачей от масштаба. В. Подиновский также предлагает промежуточную модель DEA, в которой есть возможность оценивать некоторые параметры входа и выхода с точки зрения постоянной отдачи от масштаба, а некоторые — с точки зрения переменной. Такой подход позволяет уменьшить разрыв между оценками, полученными с помощью разных моделей DEA.
В модели DEA существует возможность оценить эффект масштаба (Scale Economies) с помощью следующей формулы:
 ,
,
где SE — эффект масштаба;
θ CRS – значение эффективности, полученное с помощью модели CRS;
θ VRS – значение эффективности, полученное с помощью модели VRS.
Модель DEA с переменной отдачей от масштаба удобнее всего иллюстрировать в случае, когда объекты имеют единственный параметр входа и выхода, например как на рисунке 2. Наиболее высокой эффективности вуз достигает в точке 3, для которой характерна максимально возможная результативность вложенного ресурса. Это случай постоянной отдачи от масштаба. Как правило, в течение жизненного цикла у университетов происходит смена эффекта масштаба. Может наблюдаться возрастающая отдача от масштаба, особенно на первых этапах введения новых образовательных продуктов или реализации научных и инновационных проектов (например, отрезок, представленный вузами 1 и 3). После достижения точки насыщения появляется убывающая отдача от масштаба (см. отрезок, который соединяет университеты под номерами 3 и 5).

Рисунок 2 – Графическое представление модели с переменной и постоянной отдачей от масштаба
Модель (3) с ограничениями (4) является ориентированной на вход, т.е. эффективность анализируется с точки зрения того, можно ли уменьшить расход ресурсов, производя при этом неизменное количество продукта. Однако эффективность можно оценивать и с точки зрения возможности повысить результаты, не наращивая при этом использование ресурсов. Для второго случая существует модель DEA, ориентированная на выход.
Вектор коэффициентов можно содержательно интерпретировать как набор теневых цен соответствующих входных и выходных параметров. Теневая цена – это максимальная стоимость, которую университет мог бы заплатить за увеличение данного параметра на единицу. Теневые цены характеризуют эффективность использования каждого из ресурсов.
При решении задачи линейного программирования (3) или (7) при ограничениях (4), (4)–(5) или (8) может иметь место неадекватное оценивание вектора теневых цен. Чтобы избежать этой ситуации, Т. Коэлли, а также многие авторы, занимающиеся эмпирическим приложением модели DEA к оценке эффективности, используют методику ценностных суждений. Суть ее заключается во введении дополнительных ограничений на элементы вектора.
 ,
,
Где linf — вектор нижних ограничений на теневые цены, а lsup — вектор верхних ограничений. С выбором данных векторов возникают определенные трудности, так как они должны отражать экспертное мнение. Как один из подходов к решению этой проблемы В. Подиновский предлагает методику установления нижних и верхних ограничений с помощью определения оптимальных обменных соотношений между параметрами входа и выхода. На практике каждый автор вводит собственные оценки.