
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Закон Гесса.
|
|
В 1836 году русским академиком Г. И. Гессом установленно опытным путём, что тепловой эффект химической реакции не зависит от пути её протекания, а определяется лишь начальным и конечным состоянием системы при p = const или V = const.
Закон Гесса дает возможность рассчитать тепловые эффекты процессов в тех случаях, когда их трудно измерить в определённых условиях или когда в этих условиях нельзя осуществить этот процесс.
Тепловой эффект реакции – максимальное количество теплоты, выделяющееся в необратимом процессе при p = const или V = const, если все вещества имеют одинаковую температуру и отсутствуют другие виды работ, кроме работы расширения.
В химической термодинамике стандартным состоянием называется состояние системы, выбираемое как точка отсчета при оценке термодинамических величин. Необходимость выбора стандартного состояния обусловлена тем, что в рамках химической термодинамики не могут быть рассчитаны абсолютные значения энергий Гиббса, энтальпий и других термодинамических функций для данного вещества. Стандартное состояние характеризуется стандартными условиями – температура 25°С (298.15 К) и давление 1 атм. Тепловые эффекты, отнесённые к этим условиям, называются стандартными тепловыми эффектами.
В качестве стандартного состояния для простых веществ принимают устойчивое фазовое и химическое состояние элемента при данной температуре.
Для расчета теплового эффекта химических реакций используют термохимическте уравнения, в которых обязательно указывается агрегатное состояние реагирующих веществ и продуктов реакции; для твеодых веществ указывается их полиморфная модификация: С графит, С алмаз. В термохимических уравнения также указывается тепловой эффект реакции или изменение энтальпии химической реакции, рассчитанное для стандартных условий.
Основу всех термохимических расчетов составляет закон Гесса, который можно представить в виде:
QV = ∆ U, V = const, (1.21)
QP = ∆ H, p = const. (1.22)
Следствия из закона Гесса:
Следствие 1. Тепловой эффект реакции равен разности сумм теплот образования продуктов реакции и сумм теплот образования исходних веществ при стандартных условиях, умноженных на соответствующие стехиометрические коэффициенты.
 =
= 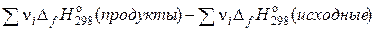 , (1.23)
, (1.23)
знак «o» означает стандартные условия, f – “formation” (образование).
Стандартная теплота образования вещества – это теплота реакции образования вещества из простых веществ, устойчивых при данных условиях.
Следствие 2. Тепловой эффект реакции при стандартных условиях равен разности между суммой теплот сгорания исходных веществ и суммой теплот сгорания продуктов реакции, умноженных на соответствующие стехиометрические коэффициенты.
 (1.24)
(1.24)
Стандартная теплота сгорания – теплота, выделяющаяся при сгорании в атмосфере кислорода 1 моля вещества при стандартных условиях до высших оксидов.Причём, все участники реакции должны быть в устойчивых агрегатных состояниях.
В химической термодинамике чаще всего рассматриваются изобарные процессы (p = const), для которых QP = ∆ H. Поэтому термин «тепловой эффект реакции» заменяют термином «энтальпия реакции». Энтальпия реакции – это изменение энтальпии системы при протекании химической реакции. Она может быть больше нуля или меньше нуля.
Если ∆ H > 0, то Q > 0 (эндотермические реакции).
Если ∆ H < 0, то Q < 0 (экзотермические реакции).
1.6. ТЕПЛОЁМКОСТЬ. УРАВНЕНИЕ КИРХГОФА.
Теплоёмкость – то количество теплоты, которое необходимо сообщить или отнять телу или системе, чтобы их температура изменилась на 1 градус. Теплоёмкость — величина экстенсивная, так как зависит от размера системы. Теплоёмкость, рассчитанная на 1 моль вещества, называется мольной, а на единицу массы – удельной.
Различают:
— истинную теплоёмкость:  [
[ 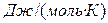 ]. (1.25)
]. (1.25)
— среднюю теплоёмкость:  . (1.26)
. (1.26)
Наиболее часто используются следующие теплоемкости:
1. Изохорная теплоемкость. При нагреве или охлаждении вещества при постоянном объеме справедливо:
. 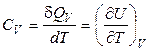 . (1.27)
. (1.27)
2. Изобарная теплоемкость. При нагреве или охлаждении вещества при постоянном давлении справедливо:
.  . (1.28)
. (1.28)
Следует знать, что теплоёмкость при постоянном давлении Ср больше, чем теплоёмкость при постоянном объёме С V, так как нагревание вещества при постоянном давлении сопровождается работой расширения, т.е.
 . (1.29)
. (1.29)
Для идеальных газов справедливо уравнение Майера:
 . (1.30)
. (1.30)
Величина R (универсальная газовая постоянная) равна работе расширения 1 моля идеального газа (при р = const) при увеличении его температуры на 1 градус.
Отношение  обозначается символом
обозначается символом  (адиабатический коэффициент), который всегда больше нуля (
(адиабатический коэффициент), который всегда больше нуля ( > 0).
> 0).
Зависимость теплоёмкости веществ в области не очень низких температур (Т ≥ 298 К) обычно выражается в виде следующих полиномов:
 . (1.31)
. (1.31)
 . (1.32)
. (1.32)
Значения a, b, c, c ´, d приведены в справочниках физико-химических и термодинамических величин.
Рассмотрим уравнение Кирхгоффа, описывающее зависимость энтальпии реакции от температуры:
 , (1.33)
, (1.33)
где
 ,
,
т. е. разность между суммой теплоёмкостей продуктов реакции и исходных веществ с учётом стехиометрических коэффициентов.
Для вычисления интеграла необходимо знать зависимость теплоёмкости от температуры для всех веществ, что не всегда возможно. Поэтому уравнение Кирхгоффа применяют в трёх приближениях.
1. При наиболее грубом приближении полагают, что D Сp = 0, т.е. считают равными суммарные теплоёмкости продуктов и исходных веществ. Тогда  ,
,
т.е. тепловой эффект считается не зависящим от температуры. Этим приближением пользуются, если теплоемкости некоторых участников реакции неизвестны.
2. Во втором приближении считают разность теплоёмкостей постоянной величиной D СР = const. Тогда
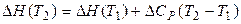 . (1.34)
. (1.34)
Это уравнение применяют только для небольшого интервала температур Т 2 – Т 1, в котором известны величины теплоёмкостей.
3. В наиболее точном приближении используют зависимость всех СРi от температуры. Если теплоемкости веществ даны в виде полиномов, например (1.34), то уравнение Кирхгоффа можно проинтегрировать, после чего оно будет иметь следующий вид:
 . (1.35)
. (1.35)
Последнее уравнение можно использовать только в том интервале температур Т 2 – Т 1, для которого определены коэффициенты a i, b i, c i температурной зависимости теплоёмкостей веществ.