Второй закон термодинамики. Энтропия.

Все процессы, протекающее в природе, подчиняются первому закону термодинамики, однако не всякий возможный процесс осуществим на практике. Исходя из первого закона, нельзя решить, происходит ли самопроизвольно переход теплоты от нагретого тела к холодному или наоборот, т.е. нельзя определить направление самопроизвольного процесса (процесса, происходящего спонтанно без внешних воздействий).

Второй закон термодинамики позволяет предсказать направление процесса при заданных условиях. В отличие от первого закона термодинамики он не носит всеобщего характера, и применим лишь к системам, состоящим из большого числа частиц.

Открытию второго закона термодинамики предшествовало изобретение тепловых машин – устройств, которые могут превращать теплоту в работу. Естественность хаотического движения молекул приводит к тому, что теплоту нельзя полностью превратить в работу. А работу можно полностью превратить в теплоту – это принципиальное отличие теплоты от работы.

Любой химический процесс можно представить как совокупность двух явлений: во-первых, передачи энергии, во-вторых, изменение упорядоченности во взаимном расположении частиц. Качественно охарактеризовать рассеивание тепловой энергии призвана энтропия, которая обозначается символом S. Энтропия – мера неупорядоченности системы. При переходе системы из более упорядоченного состояния в менее упорядоченное состояние энтропия системы возрастает, а при переходе системы из менее упорядоченного в более упорядоченное состояние энтропия системы уменьшается.

Существует несколько формулировок второго закона термодинамики:

1. Формулировка по Клаузиусу. Теплота не может самопроизвольно переходить от более холодного тела к более горячему.

2. Формулировка по Оствальду. Вечный двигатель второго рода невозможен (т.е. не существует машины, которая бы полностью превращала теплоту в работу).

3. Формулировка по Томсону. Невозможно получать работу при наличии только одного источника тепла в циклически действующей машине.

В тепловых машинах вещество (рабочее тело) совершает цикл процессов, возвращаясь в исходнее состояние. Простейшим примером является цикл Карно (рабочее тело – идеальный газ), который состоит из двух изотерм и двух адиабат. Используя цикл Карно, можно доказать, что приведенная теплота Q / T обладает свойствами функции состояния. Энтропия также является функцией состояния (так как число способов, которыми можно реализовать то или иное состояние, не зависит от пути перехода в него) и её изменение в любом равновесном (обратимом) процессе равно приведённой теплоте:

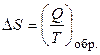, (2.1)

или

. (2.2)

Следует учитывать, что для необратимых процессов приведённая теплота не является функцией состояния и

. (2.3)

Итак, второй закон термодинамики гласит: в изолированной системе самопроизвольно протекает только такие процессы, которые ведут к увеличению неупорядоченности системы, т.е. к росту энтропии. Основной смысл этого закона состоит в том, что в любой изолированной системе с течением времени происходит постоянное возрастание степени беспорядка, а, значит, и рост энтропии.

Или: существует функция состояния S – энтропия, которая следующим образом связана с теплотой, поступающей в систему, и температурой системы:

1. – для самопроизвольных процессов;

2. – для обратимых (равновесных) процессов;

3. – для несамопроизвольных процессов,

т. е. второй закон термодинамики для различных процессов можно записать с помощью трёх вышеуказанных уравнений.

В изолированной системе (δ Q = 0 ) и изменение энтропии служит критерием направления процесса, т. е. является критерием обратимости и необратимости процессов: если в процессе dS > 0, то он самопроизволен, необратим, а если dS = 0, то он равновесный, обратимый. Энтропия изолированной системы или увеличивается, или остаётся постоянной, и в состоянии равновесия энтропия максимальна: S _{u, v} = S _max и (∆ S)_{u, v} = 0.

Следует отметить, что если процесс протекает в неизолированной системе, то для оценки необратимости процесса необходимо иметь величину изменения энтропии системы и величину изменения энтропии окружающей среды.

2.2. РАСЧЁТ ИЗМЕНЕНИЯ ЭНТРОПИИ ДЛЯ РАЗЛИЧНЫХ ПРОЦЕССОВ. ПОСТУЛАТ ПЛАНКА.

2.2.1. Расчёт энтропии для равновесных (обратимых) процессов.

Второй закон термодинамики в виде , записанный для равновесных процессов, позволяет вычислить не абсолютное значение энтропии, а только разность энтропий в двух состояниях системы.

. (2.4)

Рассмотрим для 1 моля вещества:

а) Изотермические процессы (T = const).

При постоянной температуре протекают процессы фазовых превращений веществ: плавление, испарение и другие. При равновесном протекании этих процессов давление сохраняется обычно постоянным, поэтому и

, (2.5)

где 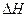– энтальпия фазового перехода.

б) Изобарные процессы (р = const).

Если нагревание происходит при постоянном давлении, то

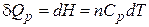, (2.6)

где n – число молей вещества. Тогда

. (2.7)

Пример 2.1. Определить изменение энтропии при нагреве 1 моль Al от 25 до 600⁰С, если для него в этом интервале теплоёмкость зависит от температуры следующим образом:

, (Дж/моль К).

Решение. Согласно уравнению (2.7) имеем:

,

(Дж/моль К).

с) Изохорные процессы (V = const).

Если нагревание происходит при постоянном объёме, то

. (2.8)

Тогда

. (2.9)

Для 1 моля идеального газа справедливо:

а) При изменении объёма и температуры

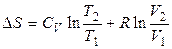, (2.10)

с учетом, что .

б) При изменении давления и температуры

. (2.11)

Для любого вещества при любой температуре можно определить и абсолютное значение энтропии, если воспользоваться постулатом Планка: энтропия правильно образованного кристалла любого индивидуального вещества при абсолютном нуле равна нулю.

Если вещество при температуре Т находится в газообразном состоянии, то его абсолютная энтропия может быть вычислена по формуле:

. (2.12)

2.2.2. Расчёт изменения энтропии в ходе химической реакции.

Расчёт изменения энтропии в ходе химической реакции проводится по формуле:

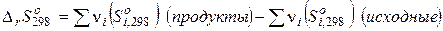, (2.13)

где - стандартные энтропии веществ при Т = 298, 15 К.

Каждое вещество характеризуется стандартной энтропией – энтропией 1 моль вещества при 298.15 К и давлении 1 атм. Значения энтропии имеют размерность Дж/(моль К) или кал/(моль К). Стандартные энтропии простых веществ не равны нулю.

2.2.3. Расчёт изменения энтропии в ходе самопроизвольных (необратимых) процессов.

Для необратимых процессов и уравнение (2.4) не применимо. Энтропия – функция состояния и её изменение не зависит от пути процесса, а определяется конечным и начальным состоянием системы. Изменение энтропии в любом неравновесном процессе можно вычислить, заменяя его некоторой совокупностью равновесных процессов, просходящими между теми же начальными и конечными состояниями, для каждого из которых можно рассчитать значение . Тогда:

. (2.14)