
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Метод основных построений
|
|
Лекция 1. Задачи на построение в курсе геометрии основной школы
Основная цель: рассмотреть с учащимися новый тип геометрических задач – задачи на построение. Сформировать умение выполнять основные построения с помощью циркуля и линейки, познакомить со структурой процесса решения задач на построение и методами их решения.
Содержание учебного материала
Первоначально с задачами на построение учащиеся знакомятся в 7 классе. В качестве инструментов построения чаще всего являются линейка и циркуль. С помощью линейки как инструмента геометрических построений можно провести произвольную прямую; произвольную прямую, проходящую через данную точку; произвольную прямую, проходящую через две данные точки. Никаких других операций выполнять линейкой нельзя.
Циркуль как инструмент геометрических построений позволяет описать из данного центра окружность данного радиуса. В частности, циркулем можно отложить данный отрезок на данной прямой от данной точки» (П., с. 58). В учебнике А. конструктивные возможности линейки и циркуля описываются несколько иначе (см. с. 44).
В геометрии среди задач на построение выделяют так называемые основные построения. Перечислим их с указанием наличия в школьных учебниках.
| Номер ОП | Название ОП | В учебнике А. | В учебнике П. |
| 1. | Построение треугольника по трём сторонам. | С.84 | С.58 |
| 2. | Построение угла, равного данному. | С. 45 | С.59 |
| 3. | Построение биссектрисы угла. | С. 46 | С.59 |
| 4. | Построение середины отрезка | С. 48 | С.59 |
| Построение прямой, перпендикулярной к данной прямой и проходящей через данную точку | С. 47, с. 49 (№ 153) | С.60 | |
| 6. | Построение прямой, параллельной данной прямой и проходящей через данную точку | С. 68 (№ 222) | |
| 7. | Построение треугольника по стороне и двум прилежащим углам. | С. 85 | С. 65, № 23 (2) |
| 8. | Построение треугольника по двум сторонам и углу между ними. | С. 84 | С. 65, № 23 (1) |
| 9. | Построение прямоугольного треугольника по гипотенузе и острому углу. | С. 92, №314(а) | |
| 10. | Построение прямоугольного треугольника по катету и гипотенузе. | С. 92, №314(в) | С. 65, № 35 |
| 11. | Построение касательной к данной окружности, проходящей через данную точку. | С. 167, С. 175, № 673 | С. 66, № 49 (2) |
| Построение окружности, вписанной в данный треугольник. | С. 186, № 701 | С. 65, № 26 | |
| 13. | Построение окружности, описанной около данного треугольника. | С. 187, № 711 | С.65, № 34 |
| 14. | Построение отрезка, четвёртого пропорционального к трём данным отрезкам. | С. 163, № 628 | С.78, Задача 6.1 |
| 15. | Построение отрезка, среднего пропорционального к двум данным отрезкам. | С. 175, № 669 | С. 95, № 15. |
| 16. | Деление отрезка на п равных частей. | С. 108, № 396 | С.74, № 48 |
| 17. | Деление отрезка в отношении т: п (внутренним и внешним образом). | С. 155, № 584 |
При изучении основных преобразований полезно предложить учащимся завести альбом и использовать следующую форму записи
Пример 1.
ОП 2. Построение угла, равного данному углу.
Построить: Ð А1В1С1. Условия: Ð АВС =Ð А1В1С1.
| Построение.
| План построения. 1. р – прямая. 2. В1 Î р. 3. Окружность (В, r). 4. М – точка пересечения окружности и ВС. 5. N – точка пересечения окружности и АВ 6.Окр. (В1, r). 7. С1 – точка пересечения окружности (6) и прямой р. 7. Окружность (С1, МN) 8. А1 – точка пересечения окружности (6) и (7) 9. В1А1. 10. Ð А1В1С1 = Ð АВС. |
Пример 2.
ОП 10.
Дано:
 Построить D АВС.
Условия:
Ð С = 90°,
АВ = с,
ВС = а. Построить D АВС.
Условия:
Ð С = 90°,
АВ = с,
ВС = а.
| Построение

| План построения. 1. Прямая l. 2. Точка СÎ l. 3. Прямая п (ОП 5). 4. Окр. (С; а). 5. Точка В= п∩ Окр.(С; а). 6. Окр. (В; с). 7. Точка А= l ∩ Окр.(В; с). 8. D АВС. |
Изучение основных построений кроме реализации геометрических целей способствует формированию алгоритмической культуры учащихся.
Кроме основных построений в геометрии 7 – 9 классов рассматриваются в явном или в неявном виде другие методы решения задач. В учебнике А. приводится схема решения задач на построение:
1. Анализ: отыскание способа решения задачи путём установления связей между искомыми элементами и данными задачи. В результате анализа составляется план построения.
2. Построение: реализация плана.
3. Доказательство того, что построенная фигура удовлетворяет условию задачи.
4. Исследование, предполагающее ответ на 2 вопроса: всегда ли задача имеет решение и если имеет, то сколько. Исследование проводится по каждому пункту плана построения.
Рассмотрим методы решения задач на построение, используемые в школе, и приведём примеры.
Метод основных построений
Его суть состоит в том, что при выполнении анализа задачи следует подобрать последовательность основных построений, приводящих к построению искомой фигуры. При решении задач этим методом полезен эвристический приём под девизом «ищи треугольник».
№ 1 (А. 351). Постройте треугольник по двум сторонам и высоте к третьей стороне.
Дано: Анализ: План построения:
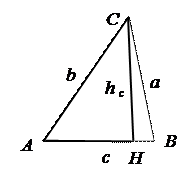
 1. D АСН (ОП 10).
1. D АСН (ОП 10).
2. ω - Окр. (С, а).
3. В = ω ∩ АН.
4. D АВС.
Построить D АВС.
Условия:
ВС = а, АС = b, DАСН – прямоугольный, он может быть
СН = h, СН ^ АВ. построен по катету НС и гипотенузе АС.
Это ОП 10. Вершина В определяется как
точка пересечения прямой АН и окр. (С, а).
 Построение
Построение
Доказательство
1. СН – высота D АВС, СН = h (по построению).
2. АС = b (по построению).
3. ВС = а (по построению).
D АВС удовлетворяет условиям построения.
Исследование
1. D АСН может быть построен, если b > hc.
3. Точка В может быть построена, если а > hc.
Задача имеет единственное решение.
№2. (А. 872). Постройте треугольник по двум сторонам и биссектрисе угла между ними.
Дано: Анализ:
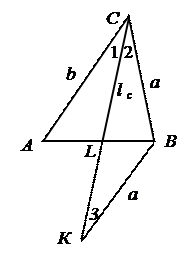
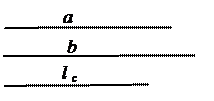
Построить DАВС.
Условия:
СВ = а; ВС = b;
СL – биссектриса угла С, СL = lc.
Попытаемся установить зависимость между а, b и lc. Для этого проведём ВК || AC до пересечения с CL.
DСКВ - равнобедренный (Ð 1=Ð 2, Ð 1=Ð 3: Ð 2=Ð 3). Его можно построить, если удастся построить LK. Так как DACL ~ DBKL, то  LK может быть построен как 4-ый пропорциональный отрезок к трём данным (ОП 14).
LK может быть построен как 4-ый пропорциональный отрезок к трём данным (ОП 14).
План построения.
1.  2. СК. 3. DСКВ 4. СА. 5. DАВС.
2. СК. 3. DСКВ 4. СА. 5. DАВС.

