В форме дифференциального уравнения

МЕТОДЫ АНАЛИЗА ЛИНЕЙНЫХ ОДНОМЕРНЫХ СИСТЕМ

Методические указания

к проведению лабораторных занятий

и контрольные задания

для самостоятельной работы

по дисциплине «Основы аналитической теории

анализа и синтеза САУ»

для студентов специальностей 210100 и 071900

и направления 550200

Одобрено

редакционно-издательским советом

Саратовского государственного технического университета

Саратов 2002 ВВЕДЕНИЕ

Одной из основных задач исследования управляемых систем является задача анализа, заключающаяся в определении закона изменения выходной величины при подаче на вход системы известного входного воздействия. Анализ проводится с использованием математической модели системы либо в форме дифференциального уравнения, либо в форме передаточной функции. В ряде случаев при анализе целесообразно использовать представление модели системы в форме Коши.

Рассматривается два раздела: анализ систем с использованием модели в форме дифференциального уравнения и применение преобразования Лапласа в анализе систем.

Лабораторные и практические занятия имеют своей целью систематизацию, закрепление и расширение теоретических знаний и получение практических навыков при решении конкретных технических задач, развитие навыков самостоятельной работы с технической литературой в ходе расчета.

Задачи, рассматриваемые в методических указаниях, соответствуют рекомендациям программы изучения дисциплины, призваны способствовать лучшему усвоению теоретического материала, изучаемого в соответствующем разделе.

Вначале рассматриваются решенные задачи, а затем приводятся задачи для самостоятельной работы, которые являются составной частью отчета по соответствующему модулю при модульно – рейтинговой системе.

АНАЛИЗ ЛИНЕЙНЫХ ОДНОМЕРНЫХ

СТАЦИОНАРНЫХ НЕПРЕРЫВНЫХ СИСТЕМ

ПРИ ДЕТЕРМИНИРОВАННЫХ ВОЗДЕЙТВИЯХ

Задача анализа заключаетя в определении закона изменения выходной величины y(t) при подаче на вход системы известного входного воздействия u(t). Анализ проводится использованием математической модели системы, как правило, либо в форме дифференциального уравнения, либо в форме передаточной функции. В ряде случаев при анализе целесообразно использовать представление модели системы в форме Коши.

Анализ систем с использованием модели

в форме дифференциального уравнения

Пусть математическая модель одномерной системы (системы с одним входом и одним выходом) имеет вид:

(1)

где y(t) – выходная переменная; u(t) – входная переменная (управление); 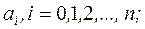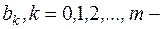постоянные коэффициенты.

Начальное состояние (положение) системы определяется начальными условиями:

(2)

Если входное воздействие u(t) задано, то правая часть уравнения (1) будет известной функцией времени (обозначим ее f(t)) и математическая модель примет вид:

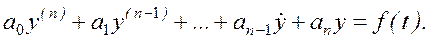(3)

Анализ заключается в решении уравнения (3) и определении y(t).

Решение линейного обыкновенного дифференциального неоднородного уравнения (3) при известных начальных условиях (2) состоит из двух составляющих:

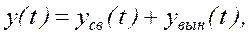(4)

где – свободная составляющая движения системы (определяется, как общее решение однородного уравнения, соответствующего неоднородному уравнению (3):

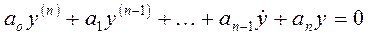. (5)

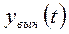– вынужденная составляющая движения (определяется, как частное решение заданного неоднородного уравнения).

Алгоритм нахождения (решение уравнения (5)).

1. Составление характеристического уравнения

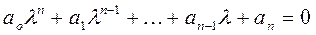. (6)

2. Нахождение собственных чисел – корней характеристического уравнения .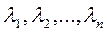

3. Запись выражения 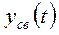по виду корней характеристического уравнения.

Пусть, например,

; – вещественные различные; – действительные одинаковые; –комплексные сопряженные, кратности 3; 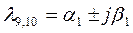– комплексные сопряженные.

Тогда в этим корням соответствуют следующие составляющие:

.

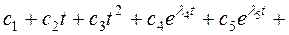
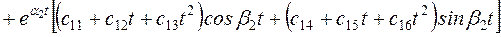Значение 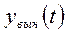может быть определено различными методами: метод вариации постоянных (метод Лагранжа), метод Коши, метод нахождения 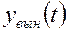по виду правой части. В большинстве практических случаев можно определить по виду правой части исходного дифференциального уравнения (3). Некоторые рекомендации по применению 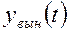приведены в приложении 1.

Записав в соответствии с (4), определяются произвольные постоянные 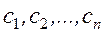из начальных условий (2).

Пример 1. [1, с. 50]. Математическая модель системы имеет вид

.

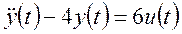Определить 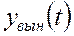, если 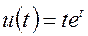, а начальные условия нулевые (система находится в покое) , .

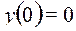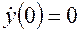Для нахождения необходимо решить дифференциальное уравнение

.

Характеристическое уравнение .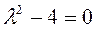

Собственные числа .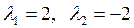

Поэтому .

Вынужденную составляющую ищем по виду правой части уравнения (приложение 1) .

Постоянные и 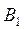определяются из условия удовлетворения 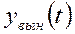исходному уравнению (модели системы).

,

.

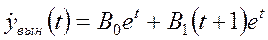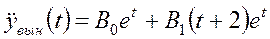Подставив 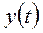, , 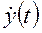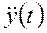и 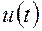в модель системы и сократив на 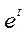, получим .

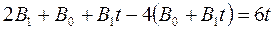Приравнивая коэффициенты при 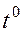и , получаем систему уравнений для определения , :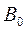

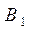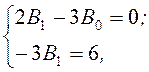
откуда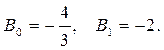

Следовательно,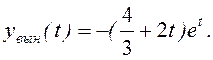

Поэтому

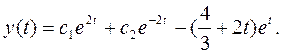
Определим произвольные постоянные из начальных условий.

Так как 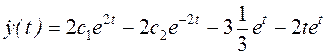, то имеем

.

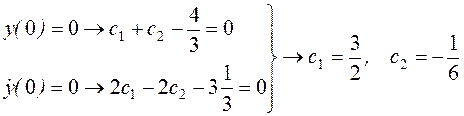Окончательно закон изменения выходной величины имеет вид

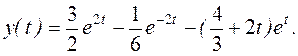
Проверка. Для того, чтобы убедиться в правильности найденного решения, подставим 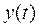в исходное уравнение. Если в результате этой подстановки получается тождество, то решение найдено верно.

Тогда подстановка в исходное уравнение дает

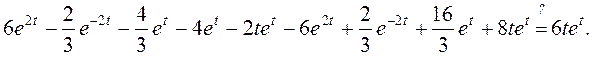
Приведя подобные в левой части, получим тождество

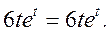
Следовательно, решение найдено верно.

Пример 2. [1, с.125]. Математическая модель системы имеет вид

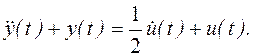
Входное воздействие . Начальные условия нулевые (система находится в покое)

Так как 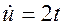, следовательно,

Поэтому модель принимает вид

Характеристическое уравнение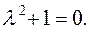

Собственные числа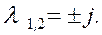

Свободная составляющая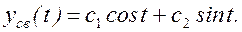

Вынужденную составляющую (частное решение неоднородного уравнения) будем искать в виде (приложение 1):

Откуда

Подставив в исходное уравнение, получим

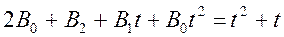
Сравнивая коэффициенты при одинаковых степенях 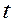, имеем

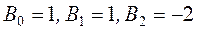
Поэтому

Следовательно,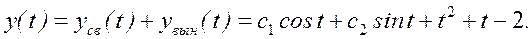

Определим 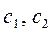из начальных условий

Окончательно закон изменения выходной переменной:

Проверка.

Подставим в исходное уравнение (модель системы):

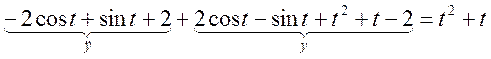
или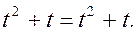

Получили тождество, что свидетельствует о том, что решение найдено верно.

Пример 3. Для электрической схемы, рис.1, определить закон изменения тока, соответствующий изменению 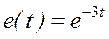при нулевых начальных условиях

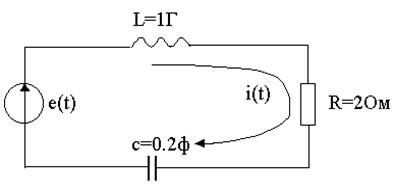
Рис.1

Из закона Кирхгофа для напряжения

и выражений

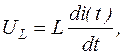
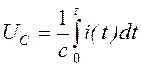
получаем математическую модель схемы в виде дифференциального уравнения:

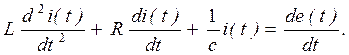
Подставив численные значения L=1Г, R=2Ом, C=0.2Ф, а также

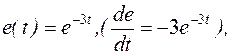получим математическую модель схемы в виде:

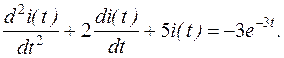
Для определения закона изменения тока i(t) необходимо решить это уравнение.

Решение уравнения ищем в виде: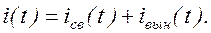

Определим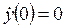

Характеристическое уравнение: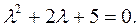

Собственные числа:

Поэтому

Определим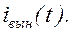

Будем искать 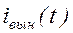в виде правой части:

Откуда

Подставим эти значения в математическую модель системы и определим А:

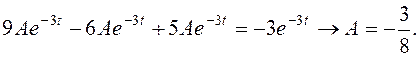
Поэтому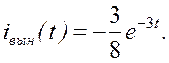

Следовательно,

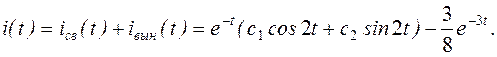
Постоянные определим из начальных условий.

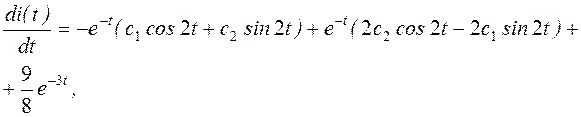
Окончательно закон изменения тока имеет вид

.

Пример 4 [2, с. 70]. Математическая модель системы имеет вид

.

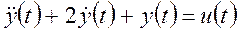Входное воздействие 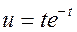. Начальные условия нулевые 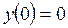, 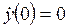. Определить закон изменения выходного сигнала .

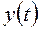Для определения надо решить уравнение вида

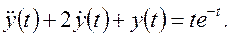
Характеристическое уравнение

.

Собственные числа 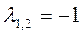– действительные одинаковые, поэтому

.

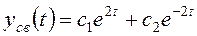Вынужденную составляющую в данном случае ищем в виде (приложение1):

,

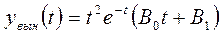так как 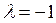является двухкратным корнем характеристического уравнения.

Постоянные 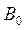, 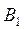определяются из условия удовлетворения дифференциальному уравнению (модели системы). Подставив в уравнение системы, получим , .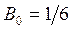

Поэтому

.

Следовательно,

.

Произвольные постоянные 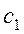, определяются из начальных условий

,

.

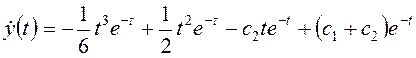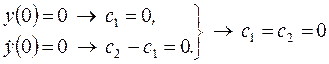Окончательно

.

Пример 5. Для электрической принципиальной схемы, рис. 2, определить закон изменения напряжения, соответствующий изменению источника тока 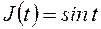. Начальные условия полагаются нулевыми .

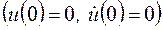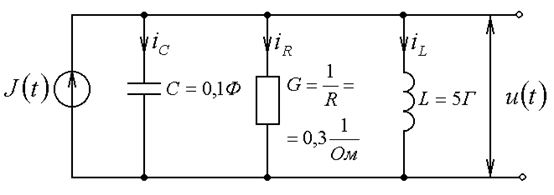
Рис.2

Из закона Кирхгофа для тока

и выражений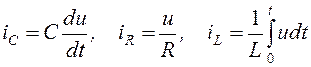

получаем математическую модель схемы в виде дифференциального уравнения

.

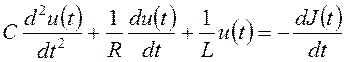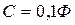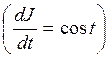Подставив численные значения параметров , , , а также , получим математическую модель в виде:

.

Закон изменения напряжения имеет две составляющие

.

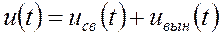Определим .

Характеристическое уравнение .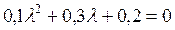

Собственные числа

Поэтому

Определим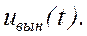

Будем искать 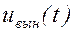в виде (приложение 1)

Откуда

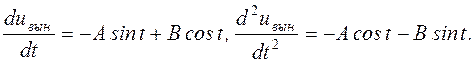
Подставим эти значения в дифференциальное уравнение и определим A, B

Поэтому

Следовательно,

Постоянные 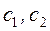определим из начальных условий

Окончательно закон изменения напряжения примет вид: