Минимизации суммы квадратов

равенства нулю суммы квадратов

минимизации модулей

равенства нулю

Решение:

При методе наименьших квадратов параметры уравнения парной линейной регрессии 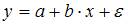определяются из условия минимизации суммы квадратов остатков .

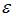Тема 6: Предпосылки МНК, методы их проверки

1. Для обнаружения автокорреляции в остатках используется …

статистика Дарбина – Уотсона

тест Уайта

критерий Гольдфельда – Квандта

тест Парка

Решение:

Для обнаружения автокорреляции остатков используется расчет статистик Дарбина – Уотсона. Тест Уайта, критерий Гольдфельда – Квандта, тест Парка применяются для обнаружения гетероскедастичности остатков.

2. Известно, что коэффициент автокорреляции остатков первого порядка равен –0, 3. Также даны критические значения статистики Дарбина – Уотсона для заданного количества параметров при неизвестном и количестве наблюдений 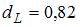, 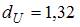. По данным характеристикам можно сделать вывод о том, что …

автокорреляция остатков отсутствует

статистика Дарбина – Уотсона попадает в зону неопределенности

есть положительная автокорреляция остатков

есть отрицательная автокорреляция остатков

Решение:

Дано, что коэффициент автокорреляции остатков первого порядка равен –0, 3, 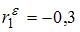. Рассчитаем статистику Дарбина – Уотсона по формуле . Нам известны критические значения статистики Дарбина – Уотсона для заданного количества параметров при неизвестном и количестве наблюдений 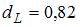, , 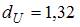которые разбивают отрезок от 0 до 4 на пять частей.

В интервале [0; 0, 82] есть положительная автокорреляция остатков;

в интервале (0, 82; 1, 32] – зона неопределенности;

в интервале (1, 32; 2, 68] нет автокорреляции остатков;

в интервале (2, 68; 3, 12] – зона неопределенности;

в интервале (3, 12; 4] есть отрицательная автокорреляция остатков.

В нашем случае значение статистики Дарбина–Уотсона d=2, 6 попадает в интервал (1, 32; 2, 68]. Значит, можно сделать вывод, что нет автокорреляции остатков.

3. Значение критерия Дарбина – Уотсона можно приблизительно рассчитать по формул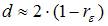е , где 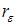– значение коэффициента автокорреляции остатков модели. Минимальная величина значения 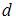будет наблюдаться при ________ автокорреляции остатков.

положительной

отрицательной

нулевой

бесконечно малой

Решение:

Значение коэффициента автокорреляции остатков модели 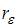рассчитывается по аналогии с парным коэффициентом автокорреляции и изменяется в таких же пределах, то есть от –1 до +1. Подставим эти граничные значения в формулу для расчета значения критерия Дарбина – Уотсона: если , то ; если , то . Поэтому значение 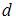меняется от 0 до 4. Минимальное значение 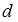равно 0 для случая, когда 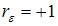, то есть для положительной автокорреляции остатков.