Тема 10: Оценка качества подбора уравнения

1. Известно, что доля остаточной регрессии в общей составила 0, 19. Тогда значение коэффициента корреляции равно …

0, 9

0, 19

0, 81

0, 95

Решение:

Известно, что доля остаточной регрессии в общей составила 0, 19. Значит, Найдем коэффициент детерминации: Вычислим коэффициент корреляции:

2. Известно, что общая сумма квадратов отклонений , а остаточная сумма квадратов отклонений, . Тогда значение коэффициента детерминации равно …

0, 8

0, 2

Решение:

Для расчета коэффициента детерминации можно пользоваться следующей формулой: 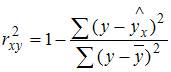. Значит, в нашем случае коэффициент детерминации равен:

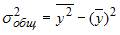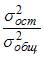3. Для регрессионной модели вида , где рассчитаны дисперсии: ; ; . Тогда величина характеризует долю …

остаточной дисперсии

коэффициента детерминации

коэффициента корреляции

объясненной дисперсии

Решение:

Значение коэффициента детерминации характеризует долю дисперсии зависимой переменной, объясненную построенным уравнением регрессии, в общей дисперсии зависимой переменной. Разность 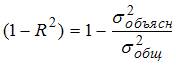характеризует долю остаточной дисперсии, которая может быть рассчитана также по формуле 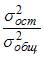. Поэтому отношение 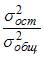характеризует долю остаточной дисперсии.

4. Если общая сумма квадратов отклонений , и остаточная сумма квадратов отклонений , то сумма квадратов отклонений, объясненная регрессией, равна …

0, 25

Решение:

Общая сумма квадратов отклонений складывается из суммы квадратов отклонений, объясненных регрессией, и остаточной сумма квадратов отклонений.

Значит, сумма квадратов отклонений, объясненная регрессией, равна разности общей сумме квадратов отклонений и остаточной суммы квадратов отклонений.

Получается .

Тема 11: Проверка статистической значимости эконометрической модели

1. При расчете скорректированного коэффициента множественной детерминации пользуются формулой 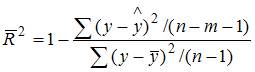, где …

n – число наблюдений; m – число факторов, включенных в модель множественной регрессии

m – число наблюдений; n – число факторов, включенных в модель множественной регрессии

n – число параметров при независимых переменных; m – число факторов, включенных в модель множественной регрессии

n – число параметров при независимых переменных; m – число наблюдений

Решение:

Скорректированный индекс множественной детерминации содержит поправку на число степеней свободы и имеет вид 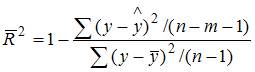, где n – число наблюдений, m – число факторов, включенных в модель множественной регрессии.

2. Если известно уравнение множественной регрессии построенное по результатам 50 наблюдений, для которого общая сумма квадратов отклонений равна 153, и остаточная сумма квадратов отклонений равна 3, то значение F-статистики равно …

766, 67

877, 45

Решение:

Расчет F -статистики начинается с разложения общей суммы квадратов отклонений на сумму квадратов отклонений, объясненную регрессией, и остаточную сумму квадратов отклонений:
, где

– общая сумма квадратов отклонений

– сумма квадратов отклонений, объясненная регрессией

– остаточная сумма квадратов отклонений

В нашем случае дано , . Следовательно,

Существует равенство между числом степеней свободы общей, факторной и остаточной сумм квадратов отклонений:

n – 1 = m + (n – m – 1 ), где n –число наблюдений, m – число параметров перед переменными в уравнений регрессии.

Число степеней свободы для общей суммы квадратов отклонений равно n – 1. В нашем случае n – 1 = 49.

Число степеней свободы для остаточной суммы квадратов отклонений равно n – m – 1 = 46.

Число степеней свободы для факторной суммы квадратов отклонений равно m = 3.

Рассчитаем факторную и остаточную дисперсии на одну степень свободы по формулам

F -статистика вычисляется по формуле

3. Для регрессионной модели известны следующие величины дисперсий:
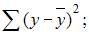
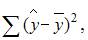где y – значение зависимой переменной по исходным данным; – значение зависимой переменной, вычисленное по регрессионной модели; 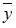– среднее значение зависимой переменной, определенное по исходным статистическим данным. Для указанных дисперсий справедливо равенство …

Решение:

Назовем приведенные дисперсии: – общая дисперсия; – объясненная дисперсия; – остаточная дисперсия. При анализе статистической модели величину общей дисперсии рассматривают как сумму объясненной и остаточной дисперсий, поэтому справедливо равенство:

Тема 12: Оценка значимости параметров эконометрической модели

1. Для уравнения множественной регрессии вида на основании 14 наблюдений рассчитаны оценки параметров и записана модель: (в скобках указаны значения t -статистики, соответствующие параметрам регрессии). Известны критические значения Стьюдента для различных уровней значимости

При уровне значимости 0, 1 значимыми являются параметры …

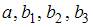
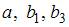
Решение:

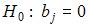Чтобы оценить значимость параметров регрессии используется t -критерий Стьюдента. Для каждого коэффициента регрессии формулируется нулевая гипотеза при альтернативной гипотезе Затем рассчитывается фактическое значение t -статистики, которое сравнивается с критическим значением Стьюдента для требуемого числа степеней свободы и уровня значимости. Если , коэффициент значим; если коэффициент незначим. В нашем случае при уровне значимости 0, 1 значимым является параметры

2. Если для среднеквадратической ошибки параметра и значения оценки этого параметра линейной эконометрической модели выполняется соотношение , то это свидетельствует о статистической ______ параметра.

ненадежности оценки

надежности оценки

ненадежности среднеквадратической ошибки

надежности среднеквадратической ошибки

Решение:

Превышение среднеквадратической ошибки параметра над значением его оценки свидетельствует о статистической ненадежности параметра.

3. Для уравнения множественной регрессии вида на основании 14 наблюдений рассчитаны оценки параметров и записана модель: (в скобках указаны значения t -статистики соответствующие параметрам регрессии). Известны критические значения Стьюдента для различных уровней значимости

Для данного уравнения при уровне значимости α =0, 05 значимыми являются параметры …

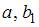
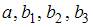
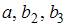
Решение:

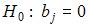Чтобы оценить значимость параметров регрессии используется t -критерий Стьюдента. Для каждого коэффициента регрессии формулируется нулевая гипотеза при альтернативной гипотезе . Затем рассчитывается фактическое значение t -статистики, которое сравнивается с критическим значением Стьюдента для требуемого числа степеней свободы и уровня значимости. Если , коэффициент значим; если коэффициент незначим. В нашем случае при уровне значимости 0, 05 значимыми является параметры

4. Проверка статистически значимого отличия от нуля оценок коэффициентов линейной модели

осуществляется путем последовательного сравнения отношений ( –среднеквадратическая ошибка параметра ) с точкой, имеющей распределение …

Стьюдента

Фишера

Дарбина – Уотсона

нормальное

Решение:

При проверке статистически значимого отличия от нуля оценок коэффициентов линейной регрессионной модели выдвигается гипотеза о нулевом значении оценки параметра. Для каждого коэффициента регрессии модели рассчитывают отношение его среднеквадратической ошибки к значению оценки . Полученное значение отношения последовательно сравнивается с точкой, имеющей распределение Стьюдента.

Тема 13: Нелинейные зависимости в экономике

1. Если зависимость объема спроса от цены характеризуется постоянной эластичностью, то моделирование целесообразно проводить на основе …

степенной функции

экспоненциальной функции

параболы второй степени

равносторонней гиперболы

Решение:

Из перечисленных функций только степенная функция характеризуется постоянной эластичностью, следовательно, ее и нужно применить для отражения данной зависимости.

2. Если по результатам анализа поля корреляции замечено, что на интервале изменения фактора меняется характер связи рассматриваемых признаков, прямая связь изменяется на обратную, то моделирование целесообразно проводить на основе …

параболы второй степени

параболы третьей степени

степенной функции

равносторонней гиперболы

Решение:

Параболу второй степени целесообразно применять в случае, когда на интервале изменения фактора меняется характер связи рассматриваемых признаков, прямая связь изменяется на обратную или обратная на прямую.