Нелинейное уравнение регрессии вида является _____ моделью ____ регрессии.

полиномиальной … парной

полиномиальной … множественной

линейной … множественной

множественной … полиномиальной

Решение:

Нелинейное уравнение регрессии вида является полиномиальной моделью парной регрессии. Теоретическое значение зависимой переменной рассчитывается в данном случае по формуле полинома третьей степени , а количество независимых переменных х равно единице.

4. Если с увеличением масштабов производства удельный расход сырья сокращается, то моделирование целесообразно проводить на основе …

равносторонней гиперболы

степенной функции

параболы второй степени

показательной функции

Решение:

Равносторонняя гипербола обычно используется в эконометрике для характеристики связи удельных расходов сырья, материалов, топлива с объемом выпускаемой продукции, поскольку она позволяет учесть эффект масштаба, что с увеличением объемов выпускаемой продукции удельные показатели расходов сырья, материалов или топлива обычно падают.

Тема 14: Виды нелинейных уравнений регрессии

1. Степенной моделью не является регрессионная модель …

Решение:

Степенной моделью регрессии является такая модель, в которой независимая переменная х стоит в основании степени, а параметр – в показателе. Такими моделями из приведенных в ответах являются уравнения: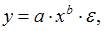

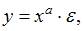
В уравнении независимая переменная х стоит в показателе степени, а параметр b – в основании, это не степенное уравнение, такая модель является примером показательной зависимости.

2. Среди предложенных нелинейных зависимостей нелинейной по параметрам является …

Решение:

Среди предложенных нелинейных зависимостей зависимость является нелинейной по параметрам, но внутренне линейной, поскольку с помощью логарифмирования ее можно привести к линейному виду. Остальные функции линейны по параметрам, но нелинейны относительно переменных и к линейному виду могут быть приведены с помощью замены переменных.

3. Среди предложенных нелинейных зависимостей нелинейной существенно (внутренне нелинейной) является …

Решение:

Среди предложенных нелинейных зависимостей зависимость является внутренне нелинейной, поскольку с помощью элементарных преобразований или замены переменных ее нельзя привести к линейному виду.

4. Среди предложенных нелинейных зависимостей внутренне линейной является …

Решение:

Среди предложенных нелинейных зависимостей зависимость является внутренне линейной, хотя она и нелинейна по переменным, поскольку с помощью логарифмирования ее можно привести к линейному виду. Остальные функции внутренне нелинейны: они не могут быть приведены к линейному виду.

Тема 15: Линеаризация нелинейных моделей регрессии

1. Для линеаризации нелинейной регрессионной модели используется …

логарифмирование

потенцирование

замена переменных

приведение уравнения к виду 1/ y

Решение:

Линеаризация – это процедура приведения нелинейной регрессионной модели к линейному виду путем различных математических преобразований. Нелинейная модель является степенной. Приведение ее к линейному виду возможно логарифмированием уравнения. Получаем Остальные виды линеаризации не позволяют линеаризовать исходную нелинейную модель.

2. Для преобразования внутренне нелинейной функции может быть применен метод …

разложения функции в ряд Тейлора

замены переменных

логарифмирования

потенцирования

Решение:

Функция является внутренне нелинейной, и для нее отсутствует прямое преобразование, которое превратит ее в линейную функцию. Только разложением функции в ряд Тейлора, то есть заменой данной функции суммой полиномов, можно привести данную функцию к линейному виду.

3. Для линеаризации нелинейной функции может быть применен метод …

логарифмирования и замены переменных

разложения функции в ряд Тейлора

потенцирования и замены переменных

обращения и замены переменных

Решение:

Функция является внутренне линейной и с помощью логарифмирования может быть преобразована к виду , которая является линейной относительно логарифмов переменных. Сделав замену переменных , , , , получим линейную функцию . Поэтому для линеаризации используется сначала логарифмирование, затем замена переменных.

Тема 16: Оценка качества нелинейных уравнений регрессии

1. При расчете уравнения нелинейной регрессии , где y – спрос на продукцию, ед.; x – цена продукции, руб., выяснилось, что доля остаточной дисперсии в общей меньше 20%. Коэффициент детерминации для данной модели попадает в отрезок минимальной длины …

[0, 8; 1]

[0, 2; 1]

[0; 0, 2]

[0; 0, 8]

Решение:

Доля остаточной дисперсии в общей меньше 20%, значит, доля объясненной регрессии в общей больше 80%, другими словами, коэффициент детерминации больше 0, 8. Поскольку коэффициент детерминации может принимать значения только в интервале [0, 1], то отрезком минимальной длины, в который попадает коэффициент детерминации для данной модели, будет отрезок [0, 8; 1].

2. По 20 регионам страны изучалась зависимость уровня безработицы y (%) от индекса потребительских цен x (% к предыдущему году) и построено уравнение в логарифмах исходных показателей: . Коэффициент корреляции между логарифмами исходных показателей составил . Коэффициент детерминации для модели в исходных показателях равен …

0, 64

0, 8

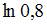
Решение:

Коэффициент детерминации для модели в исходных показателях в данном случае будет равен коэффициенту детерминации для модели в логарифмах исходных показателей, который вычисляется как квадрат коэффициента корреляции, то есть 0, 64.

3. Для регрессионной модели , где – нелинейная функция, 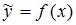– рассчитанное по модели значение переменной , получены значения дисперсий: . Не объяснена моделью часть дисперсии переменной , равная …

0, 096

0, 904

0, 106

10, 4

Решение:

Значение индекса детерминации R² характеризует долю дисперсии зависимой переменной, объясненную независимой переменной (построенным нелинейным уравнением регрессии). Разность (1-R²) характеризует долю дисперсии зависимой переменной, необъясненную уравнением, эту величину и необходимо определить в задании. Воспользуемся формулой для расчета R²: . Следовательно, разность . Таким образом, часть дисперсии переменной , необъясненная моделью, равна 0, 096. Можно также рассчитать это значение через отношение

4. Для регрессионной модели , где – нелинейная функция, 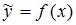– рассчитанное по модели значение переменной , получено значение индекса корреляции R = 0, 64. Моделью объяснена часть дисперсии переменной , равная …

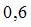
Решение:

Величина, характеризующая долю дисперсии зависимой переменной, объясненную независимой переменной (построенным нелинейным уравнением регрессии), называется индексом (коэффициентом) детерминации – R². Значения индекса детерминации R² и индекса корреляции R для нелинейных регрессионных моделей связаны соотношением . Следовательно, значение .

5. По результатам проведения исследования торговых точек было построено уравнение нелинейной регрессии , где y – спрос на продукцию, ед.; x – цена продукции, руб. Если фактическое значение t-критерия Стьюдента составляет –2, 05, а критические значения для данного количества степеней свободы равны , , , то …

при уровне значимости можно считать, что эластичность спроса по цене составляет –0, 8

при уровне значимости можно считать, что эластичность спроса по цене составляет –0, 8

эластичность спроса по цене составляет –0, 8

при уровне значимости можно считать, что эластичность спроса по цене составляет –0, 8

Решение:

Для проверки значимости коэффициентов нелинейной регрессии, после линеаризации, как и для уравнения парной линейной регрессии, применяется стандартный алгоритм критерия Стьюдента. Для b формулируется нулевая гипотеза при альтернативной гипотезе . Затем рассчитывается фактическое значение t -статистики, которое сравнивается с критическим значением Стьюдента для требуемого числа степеней свободы и уровня значимости. Если , коэффициент значим; если 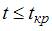, коэффициент незначим. В нашем случае при уровне значимости коэффициент значим, а при уровнях значимости и незначим.

Тема 17: Временные ряды данных: характеристики и общие понятия