Класичний закон додавання швидкостей

І. Для прямих перетворень Галілея, що описують положення точки відносно рухомої системи відліку :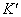

.

Продиференціюємо це співвідношення по часу:

,

тоді одержимо закон додавання швидкостей відносно рухомої системи відліку:

,

де - швидкість руху точки в системі 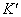(рухомій)

- швидкість руху точки в нерухомій системі .

- швидкість системи 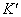відносно .

ІІ. Для обернених перетворень Галілея, що описують положення точки відносно нерухомоїсистеми:

,

тоді

.

Одержимо закон додавання швидкостей відносно нерухомої системи відліку:

ІІІ. З перетворень Галілея випливає, що прискорення точки, якщо воно існує, буде однаковим в обох інерціальних системах і 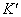. Покажемо це.

Продиференціюєм співвідношення для швидкостейвідносно нерухомої системи відліку по часу:

,

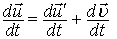Величина бо const. Тому

.

Отже, прискорення матеріальної точки чи тіла в різних інерціальних системах відліку є однаковим.