
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Релятивістський закон додавання швидкостей
|
|
Нехай система  рухається відносно
рухається відносно  з швидкістю
з швидкістю 
 так, що
так, що  . В системі
. В системі  вздовж
вздовж  рухається точка
рухається точка  . ЇЇ швидкість
. ЇЇ швидкість  . Знайдемо швидкість
. Знайдемо швидкість  цієї точки в системі
цієї точки в системі  . Для безконечно малих змін координати і часу
. Для безконечно малих змін координати і часу 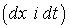 перетворення Лоренца співпадають з перетвореннями для самих координат і часу:
перетворення Лоренца співпадають з перетвореннями для самих координат і часу:

Враховуючи, що
 ,
,
вираз для швидкості в нерухомій системі відліку матиме вигляд:
 .
.
Розділимо чисельник і знаменник дробу на  :
:
 ,
,
або
 .
.
Одержали релятивістський закон додавання швидкостей відносно нерухомої системи відліку.
Висновки з формули:
1. Якщо швидкість матеріальної точки у рухомій системі відліку рівна швидкості світла (  ), тоді
), тоді
 .
.
Отже, відносно нерухомої системи відліку швидкість матеріальної точки також рівна швидкості світла.
2. Якщо швидкість рухомої системи рівна швидкості світла (  ), тоді
), тоді
 .
.
Отже, і в цьому випадку відносно нерухомої системи відліку швидкість матеріальної точки також рівна швидкості світла.
3. Виходячи з двох попередніх висновків – швидкість матеріального об’єкта не може перевищувати швидкості світла.. Релятивістський імпульс
В класичній механіці імпульс визначається:
 .
.
Відповідно до теорії відносності Ейнштейна, при великих швидкостях, маса рухомого тіла визначається виразом:
 .
.
Тому релятивістський імпульс можна записати у вигляді:
 .
.
Залежність імпульсу тіла від його швидкості показана на рис. 4.

|
Рис. 4
1-класичний випадок(  ),
),
2-релятивістський випадок.
Зауваження:
1. При швидкостях  релятивістський імпульс переходить в класичний вираз і графіки 1 і 2 співпадають.
релятивістський імпульс переходить в класичний вираз і графіки 1 і 2 співпадають.
2. При  значення релятивістського імпульсу прямує до безконечності (
значення релятивістського імпульсу прямує до безконечності (  ).
).