
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Законы сложения
|
|
Изложенный в предыдущем пункте подход к сложению целых неотрицательных чисел позволяет обосновать известные законы сложения: переместительный и сочетательный.
Докажем сначала переместительный закон, т. е. докажем, что для любых целых неотрицательных чисел а и Ь выполняется равенство а + 6 = 6 + а.
Пусть а — число элементов в множестве А, Ь — число элементов в множестве В и Af\B—0. Тогда по определению суммы целых неотрицательных чисел а-\-Ь есть число элементов объединения множеств А и В: a~\-b = n (A\JB). Но множество А[}В равно множеству В[}А согласно переместительному свойству объединения множеств, и, значит, п (А[]В) = п (В[]А). По определению суммы п (B{A)~b-\-a, поэтому а + 6 = 6 + а для любых целых неотрицательных чисел а и Ь.
Докажем теперь сочетательньцй закон, т. е. докажем, что для
любых целых неотрицательных чисел выполняется равенство
(a + b) + c = a + (b-\-c). " ' -v< l|^
Пусть а = п(А), Ь = п(В), с = п (С), причем Л? |15^ь0, Bf\C=0.
Тогда по определению суммы двух чисел можно записать (а + £ >) +
А (С) ((АВ)С)
Так как объединение множеств подчиняется сочетательному закону, то п ((Л [}В)[)С) = п (A[}(B\JC))- Откуда по определению суммы двух чисел имеем п (Л (]{В[]С)) = п (А) + п (В[]С) = а + (Ь + с). Следовательно, (а + 6) + с = а + (Ь + с) для любых целых неотрицательных чисел а, Ь и с.
Каково назначение сочетательного закона сложения? Он объясняет, как можно находить сумму трех слагаемых: для этого достаточно сложить первое слагаемое со вторым и к полученному числу прибавить третье слагаемое или прибавить первое слагаемое к сумме второго и третьего. Заметим, что сочетательный закон не предполагает перестановки слагаемых.
И переместительный и сочетательный законы сложения могут быть обобщены на любое число слагаемых. При этом переместительный закон будет означать, что сумма не изменяется при любой перестановке слагаемых, а сочетательный — что сумма не изменяется при любой группировке слагаемых (без изменения их порядка).
Из переместительного и сочетательного законов сложения вытекает, что сумма нескольких слагаемых не изменится, если их переставить любым способом и если любую их группу заключить в скобки.
Вычислим, используя законы сложения, значение выражения 109 + 36+191+64 + 27.
На основании переместительного закона переставим слагаемые 36 и 191. Тогда 109 + 36+191+64 + 27=109+191+36 + 64 + 27.
Воспользуемся сочетательным законом, сгруппировав слагаемые, а затем найдем суммы в скобках: 109+ 191 +36 + 64 + 27 = (109 + + 191) + (36 + 64) + 27 = 300+100 + 27.
Применим еще раз сочетательный закон, заключив в скобки сумму чисел 300 и 100: 300+100+ 27 = (300+100)+ 27.
Произведем вычисления: (300+100)+ 27 = 400+ 27 = 427.
С переместительным свойством сложения учащиеся начальных классов знакомятся при изучении чисел первого десятка. Сначала оно используется при составлении таблицы сложения однозначных чисел, а затем для рационализации различных вычислений.
Сочетательный закон сложения в начальном курсе математики в явном виде не изучается, но постоянно используется. Так, он является основой приема прибавления числа по частям: 3 + 2 = 3 + (1 + 1) = (3+ 1)+ 1 =4+ 1 =5. Кроме того, в тех случаях, когда надо прибавить число к сумме, сумму к числу, сумму к сумме, сочетательный закон используется в сочетании с переместительным. Например, прибавлять сумму 2+1 к числу 4 предлагается следующей способами:
1) 4+(2+1)=4+3=7
2) 4+(2+1)=6+1=7
3) 4+(2+1)=5+2=7
Понятие целых неотрицательных чисел может быть определено по-разному. Рассмотрим сначала подход, в основе которого лежит понятие суммы.
Определение: Произведением целых неотрицательных чисел а и b называется такое целое неотрицательное число а-b, которое удовлетворяет следующим условиям:

b слагаемых 2. a • 1= а при b = 1; 3.a-0 = 0 при b = 0.
Теоретико-множественный смысл этого определения следующий. Если множества Al, A2,..., АЬ имеют по а элементов каждое и никакие два из них не пересекаются, то их объединение содержит а • b элементов. Следовательно, произведение а • b — это число элементов в объединении b попарно непересекающихся множеств, каждое из которых содержит по а элементов.
Действие, при помощи которого находят произведение а и b называют, называют умножением; числа, которые умножают, называют множителями.
Произведение любых целых неотрицательных чисел существует, но оно единственно.
С данным определением учащиеся знакомятся в начальных классах. Смысл его раскрывается при решении простых задач.
Рассмотрим, например, такую задачу: «На каждое детское пальто нужно пришить 4 пуговицы. Сколько пуговиц нужно пришить на 6 таких пальто?»
Почему она решается умножением? Потому, что в ней требуется найти число элементов в объединении, состоящем из 6 множеств, в каждом из которых по 4 элемента. Согласно определению это число находится умножением: 4 * 6 = 24 (пуговицы).
Имеется и другое определение произведения целых неотрицательньтх чисел. Оно связано с декартовым произведением множеств.
Пусть даны два множества: А = { х, у, z } и В = { n, t, r, s }. Найдем их декартово произведение, которое запишем в виде прямоугольной таблицы:
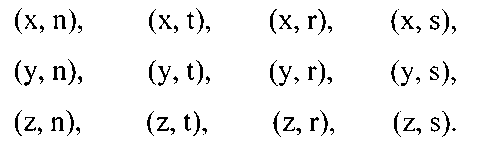
В каждой строке таблицы все пары имеют одинаковую первую компоненту, а в каждом столбце одинаковая вторая компонента. При этом никакие две строки не имеют хотя бы одной одинаковой пары. Отсюда следует, что число элементов в декартовом произведении А; * В равно 3 + 3 + 3 + 3 = 12. С другой стороны, п (А) = 3, п (В) = 4 и 3-4 =12. Видим, что число элементов в декартовом произведении данных множеств А и В равно произведению п (А) ■ п(В).
Вообще, если А и В - конечные множества, то

Таким образом, произведение целых неотрицательных чисел а и b можно рассматривать как число элементов декартова произведения множеств А и В, где п (А) = а, п(В) = Ь:

И в первом, и во втором случае нами определено произведение двух чисел. А как определить произведение нескольких множителей?
Пусть в произведении двух множителей определено и определено произведение п множителей. Тогда произведение, состоящее из п + 1 множителя, т. е. произведение al • а2 •... • а п • а п + 1, равно (al • а2 •... • an) • S an+1.
Например, чтобы найти произведение 2 • 7 -5 • 9 согласно этомуопределению, надо выполнить последовательно следующие преобразования: 2 * 7 -5 • 9 = (2 • 7 * 5) • 9 = ((2 • 7) • 5) • 9 = (14 • 5) • 9 = 70 • 9 = 630.
Законы умножения:
Докажем законы умножения исходя из определения произведения через декартово произведение множеств.
Коммутативный или переместительный закон: для любых целых неотрицательных чисел а и b справедливо равенство а • b = а ■ Ь.
Пусть а = п (А), Ь = п(В). Тогда по определению произведения а • b = п (АКВ). Но множества АХ В и ВхА равномощны: каждой паре (a, b) из множества АХВ, и наоборот. Значит, п (АхВ) = п (ВХА), и поэтому а • b = n (АхВ) = п (В А) = b • а.
Ассоциативный или сочетательный закон: для любых целых неотрицательных чисел а, Ь, с справедливо равенство (а • b) ■ с = а • (Ь-с)
Пусть a = n(A), b = n(B), с = п (С). Тогда по определению произведения (а • b) • с = п ((АХВ ЖС), а а • (b • с) = п (АX (ВХС)). Множества (АХВ) у С и АУ (ВХС) различны: первое состоит из пар вида ((a, b), (с), а второе — из пар вида (а, (Ь, с)), где а£ А, Ь€.В, сеС. Но множества (АХВ) С и АХ(В)< С) равномощны так как существует взаимно однозначное отображение одного множества на другое. Поэтому п ((АХВ)ХХ) = п (АХ(ВХС)), и, значит, (а • b)-c = a-(b-c).