
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Емпірична модель множинної лінійної регресії.
|
|
Емпірична модель являє собою статистичний аналог теоретичної моделі (2.2). За її допомогою визначаються статистичні оцінки параметрів  . При цьому використовується статистична обробка вибірки.
. При цьому використовується статистична обробка вибірки.
В загальному вигляді емпірична модель записується як:

| (2.6) |
У векторно-матричній формі система (2.6) має вигляд:

| (2.7) | |
| де | 
| |
Компоненти  вектора
вектора  є статистичними оцінками компонент
є статистичними оцінками компонент  теоретичного вектора
теоретичного вектора 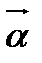 лінійної множинної регресії (2.4), а компоненти
лінійної множинної регресії (2.4), а компоненти  вектора похибок
вектора похибок 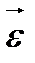 – статистичні оцінки випадкових збудників
– статистичні оцінки випадкових збудників  вектора
вектора  .
.
Якщо теоретичний вектор  є величиною сталою і нам невідомою, то емпіричний вектор
є величиною сталою і нам невідомою, то емпіричний вектор  ми можемо визначити шляхом обробки статистичної інформації вибірки обсягом
ми можемо визначити шляхом обробки статистичної інформації вибірки обсягом 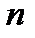 . Враховуючи те, що вибірка складає лише незначну частину генеральної сукупності
. Враховуючи те, що вибірка складає лише незначну частину генеральної сукупності  , то інформація, яку одержимо при статистичній обробці, про регресори
, то інформація, яку одержимо при статистичній обробці, про регресори  моделі буде не повною і для кожної іншої вибірки буде потерпати певні зміни. Отже, компоненти
моделі буде не повною і для кожної іншої вибірки буде потерпати певні зміни. Отже, компоненти  емпіричного вектора
емпіричного вектора 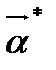 будуть містити елемент випадковості. Таким чином,
будуть містити елемент випадковості. Таким чином,  , як і сам вектор
, як і сам вектор 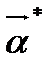 будуть випадковими величинами, які мають певні закони розподілу ймовірностей із відповідними числовими характеристиками.
будуть випадковими величинами, які мають певні закони розподілу ймовірностей із відповідними числовими характеристиками.
Із вище наведеного можемо тепер стверджувати, що  є статистичною оцінкою для теоретичного вектора
є статистичною оцінкою для теоретичного вектора  . А тому постають питання математичної статистики: зміщена чи незміщена ця статистична оцінка; в якому довірчому інтервалі із заданою надійністю γ можуть перебувати теоретичні компоненти (параметри)
. А тому постають питання математичної статистики: зміщена чи незміщена ця статистична оцінка; в якому довірчому інтервалі із заданою надійністю γ можуть перебувати теоретичні компоненти (параметри)  і сама функція регресії; як здійснити перевірку на статистичну значущість теоретичних параметрів
і сама функція регресії; як здійснити перевірку на статистичну значущість теоретичних параметрів  по заданому рівню значущості α.
по заданому рівню значущості α.
Для вирішення цих питань нам необхідно визначити числові характеристики для параметрів  (j=0, 1, 2,..., m) і для самої функції регресії, використовуючи при цьому елементи матричної алгебри як інструментарію, застосовуючи який ми можемо без громіздких викладок отримати необхідні результати.
(j=0, 1, 2,..., m) і для самої функції регресії, використовуючи при цьому елементи матричної алгебри як інструментарію, застосовуючи який ми можемо без громіздких викладок отримати необхідні результати.