
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Залежна змінна для такої моделі розглядається, як ендогенна змінна, а незалежні змінні – як екзогенні.
|
|
Теоретична (“канонічна”) загальна лінійна економетрична модель може бути специфікована у наступній формі:
 , (1)
, (1)
де: y – залежна (пояснювана) змінна моделі, x1, x2, …, xm – незалежні (пояснюючі) змінні моделі або фактори, β 0, β 1, …., β m – параметри моделі, ε – стохастична складова моделі, m – кількість пояснюючих змінних моделі. Зазначимо, що параметри β 1, β 2, …, β m ще прийнято називати коефіцієнтами регресії,
Теоретична модель (1) є гіпотетичною конструкцією і дійсна, як це відмічалося у попередній темі, для всієї генеральної сукупності спостережень за змінними моделі. Невідомі параметри  цієї моделі є константами, а випадкова величина ε – взагалі неспостережувана і ми можемо зробити тільки припущення щодо закону її розподілу.
цієї моделі є константами, а випадкова величина ε – взагалі неспостережувана і ми можемо зробити тільки припущення щодо закону її розподілу.
Вибіркова (емпірична) загальна лінійна економетрична модель має наступний вигляд:
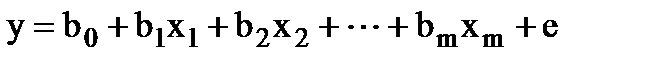 , (2)
, (2)
де: y – залежна (пояснювана) змінна моделі, x1, x2, …, xm – незалежні (пояснюючі) змінні моделі (фактори), b0, b1, bm – параметри вибіркової моделі, e – залишки моделі.
Вибіркова модель (2) є реальною конструкцією і будується на основі певної статистичної вибірки з генеральної сукупності. На відміну від моделі (1) параметри вибіркової моделі b0, b1, …, bm є оцінками (наближеними значеннями) параметрів β 0, β 1, β m і випадковими величинами, а залишки e можна оцінити (розрахувати) на основі статистичних даних. Таким чином, вибіркова модель завжди є тільки оцінкою (вдалою або невдалою) реальної але невідомої теоретичної моделі.
Вибіркова (емпірична) функція регресії для загальної лінійної економетричної моделі має наступний вигляд:
 , (3)
, (3)
де:  – оцінка математичного сподівання залежної (пояснюваної) змінної моделі, x1, x2, …, xm – незалежні (пояснюючі) змінні моделі (фактори), b0, b1, bm – параметри вибіркової регресії.
– оцінка математичного сподівання залежної (пояснюваної) змінної моделі, x1, x2, …, xm – незалежні (пояснюючі) змінні моделі (фактори), b0, b1, bm – параметри вибіркової регресії.
Для побудови і аналізу загальної лінійної економетричної моделі широко застосовується апарат матричної алгебри. Тому для подальших викладок подамо загальну лінійну економетричну модель у матричній формі. Оскільки теоретична модель використовується для канонічного подання деякого економічного явища або процесу, а реально ми оперуємо у процесі дослідження цього явища (процесу) тільки вибірковою моделлю, саме вибіркову модель подамо у матричному вигляді:
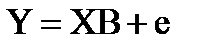 , (4)
, (4)
де:
 – вектор спостережень за залежною змінною моделі;
– вектор спостережень за залежною змінною моделі;
 -матриця спостережень за пояснюючими змінними моделі, яку ще називають регресійною матрицею;
-матриця спостережень за пояснюючими змінними моделі, яку ще називають регресійною матрицею;
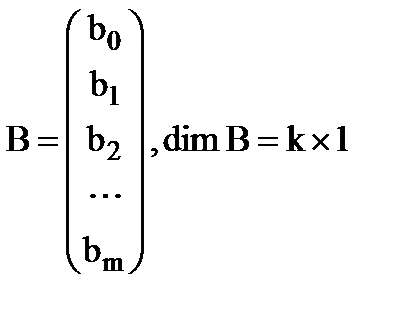 - вектор оцінок параметрів моделі (вектор параметрів вибіркової моделі);
- вектор оцінок параметрів моделі (вектор параметрів вибіркової моделі);
 - вектор залишків моделі.
- вектор залишків моделі.
Для всіх наведених вище форм представлення загальної лінійної моделі прийняті наступні загальні позначення, які будуть у подальшому постійно використовуватися:
n – розмір статистичної вибірки (кількість спостережень в статистичній вибірці);
m – число незалежних (пояснюючих) змінних моделі;
k = m + 1 – число параметрів моделі.
Найпростішою серед лінійних економетричних моделей є модель парної лінійної регресії (або проста лінійна модель), яка описує зв’язок всього між двом економічними змінними - показниками.
a Означення 2. Економетричною моделлю парної лінійної регресії (простою лінійною моделю) називається регресійна модель, яка описує лінійний зв’язок між двома економічними показниками, один з яких є залежною (пояснюваною), а другий – незалежною (пояснюючою) змінною.
Виходячи з вище розглянутих позначень для простої лінійної регресії маємо: