Зведення нелінійних економетричних моделей до лінійного вигляду

Вплив багатьох чинників на результативну змінну може бути описаний лінійною моделлю:

(2.8)

де y – досліджувана (залежна, пояснювана) змінна, або регресанд;

х₁, x₂,..., х_m – незалежні, пояснюючі змінні, або регресори;

α ₁, α ₂,..., α _m – параметри моделі;

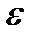– випадкова складова регресійного рівняння.

Функція (2.8) є лінійною відносно незалежних змінних і параметрів моделі, але саме лінійність за параметрами є більш суттєвою, оскільки це пов’язано з методами оцінювання параметрів. Випадкова складова ɛ є результативною дією всіх неконтрольованих випадкових факторів, що зумовлюють відхилення реальних значень досліджуваного показника y від аналітичних (обчислених на підставі обраної регресійної залежності).

Зрозуміло, що лінійні зв’язки не вичерпують усіх можливих форм залежності між показниками. Тому при дослідженні конкретного економічного явища першочерговим завданням є пошук найточнішої аналітичної форми опису статистичного зв’язку між його показниками. Певна форма залежності повинна мати відповідне економічне обґрунтування. Якщо вигляд залежності встановити важко, то за перше наближення до моделі все ж обирають лінійну залежність.

Звичайним математичним підходом до розв'язання задач є виокремлення специфічних класів задач або зведення задач до деякого класу і застосування відповідних методів розв'язування. Оскільки дослідження лінійних функцій має незаперечні переваги перед іншими класами функцій, то нелінійні функції намагаються передусім звести до лінійних. Наприклад, степенева функція:

(2.9)

після логарифмування набирає вигляду

(2.10)

і після заміни ln α _і = α _і^*, і=1, 2, …, m є лінійною відносно параметрів α ₁^*, α ₂^*,..., α _m^*. Показникова функція

(2.11)

після логарифмування набирає вигляду

(2.12)

і після заміни ln х_i = β _i, i =1, 2, …, m є лінійною відносно параметрів β _i.

Гіперболічна

(2.13)

і квадратична

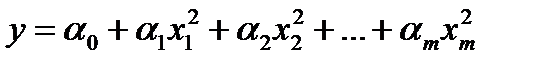
(2.14)

функції заміною змінних або зводяться до лінійного вигляду

(2.15)

Таким чином, таблиця переходів від змінних нелінійних функцій до нових змінних лінеаризованих економетричних моделей набуває наступного вигляду.

Таблиця 2.1