Оператор оцінювання 1МНК.

В основу методу найменших квадратів покладено критерій, згідно якого, „найкращою” серед усіх можливих вважається функція регресії з такими параметрами, для якої сума квадратів залишків є мінімальною. У математичному вигляді цей критерій має наступний вигляд:

. (13)

Використовуючи цей критерій і визначаються параметри вибіркової лінійної моделі.

Подамо рівняння (4) у вигляді: . Тоді суму квадратів залишків e можна записати таким чином:

. (14)

Для мінімізації суми квадратів залишків візьмемо похідну від виразу (14) за вектором оцінок параметрів В і прирівняємо похідні до нуля:

. (15)

З виразу (15) маємо:

. (16)

Вираз (16) представляє собою матричну форму запису так званої системи нормальних рівнянь. Розв’язавши її відносно вектора оцінок В отримаємо оцінку параметрів моделі. З цією метою помножимо обидві частини виразу (16) на обернену матрицю :

. Оскільки , де E – одинична матриця остаточно отримуємо:

. (17)

Таким чином, сформувавши на основі статистичної вибірки вектор спостережень за залежною змінною моделі Y і матрицю спостережень за незалежними змінними моделі X, за формулою (17) можна обчислити вектор оцінок параметрів моделі B.

Для зручності використання виразу (17) розпишемо у розгорнутій формі матриці та :

, (18)

.

. (19)

Підсумовуючи можна рекомендувати наступну послідовність кроків оцінювання параметрів загальної лінійної економетричної моделі на основі деякої статистичної вибірки:

1) формування вектору спостережень за залежною змінною моделі Y;

2) формування матриці спостережень за незалежними змінними моделі X;

3) формування матриці на основі залежності (18);

4) формування матриці 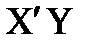на основі залежності (19);

5) визначення оберненої матриця ;

6) визначення вектору оцінок параметрів моделі В як добутку матриць і згідно виразу (17).

i Зауваження 1. У випадку парної лінійної регресії оператор оцінювання (16) значно спрощується і оцінки параметрів β ₀ і β ₁ можна визначити за наступними простими формулами:

, (20)

, (21)

де: - вибірковий коефіцієнт коваріації,

- вибіркова дисперсія пояснюючої змінної моделі,

- середнє значення пояснюючої змінної x, - середнє значення залежної змінної y.

Слід зазначити, що рівняння регресії, параметри якого оцінені методом найменших квадратів, має декілька корисних властивостей, які використовуються у практичних дослідженнях.

1. Пряма регресії (поверхня або гіперповерхня регресії) проходить через середню точку з координатами .

2. Середнє значення оцінки залежної змінної дорівнює фактичному середньому значенню, тобто .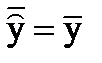

3. Сума залишків моделі дорівнює нулю, тобто .