Г). Коефіцієнт детермінації.

Коефіцієнт детермінації використовується як критерій адекватності (відповідності) моделі статистичним даним, оскільки він є мірою пояснювальної сили незалежних змінних і показує, яка частина варіації залежної змінної пояснюється саме варіацією (зміною) незалежних змінних, а не іншими випадковими факторами, які акумулюються у стохастичній складовій моделі. Іншими словами, коефіцієнт детермінації показує наскільки значним є вплив пояснюючих змінних моделі на залежну. Якщо цей вплив є значним, то побудована модель дійсно описує лінійну залежність між відповідними економічними показниками і ця залежність є суттєвою. Якщо ж цей вплив є незначним модель є неадекватною статистичним даним і лінійна регресійна залежність між економічними показниками у ній є достатньо сумнівною і неякісною.

P Суть коефіцієнта детермінації і його застосування у якості критерію адекватності можна пояснити на основі дисперсійного аналізу загальної лінійної моделі. Докладно дисперсійний аналіз загальної лінійної регресії і його зв'язок з коефіцієнтом детермінації наведено у [12, с.53-57, с.60-63, с.180-184], [15, с.111-112]. При вивчені цього питання також необхідно розібратися з такими елементами дисперсійного аналізу як SST, SSR, SSE, MSR і MSE, а також з напрямками їх застосування.

Позначається коефіцієнт детермінації через R² і обчислюється за наступною залежністю:

. (35)

Зазначимо також, що коефіцієнт детермінації може обчислюватися і за іншими формулами. Так у математичній статистиці доведено, що коефіцієнт детермінації і коефіцієнт множинної (парної) кореляції пов’язані наступним співвідношенням:

(для множинної регресії), (36)

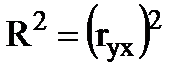(для парної регресії). (37)

Таким чином у практичних розрахунках достатньо обчислити тільки коефіцієнт кореляції, а значення коефіцієнта детермінації обчислюється на основі співвідношення (34) або (35).

Як видно з виразів (33), (34) і (35) коефіцієнт детермінації завжди є додатною величиною і може змінювати своє значення у межах від 0 до 1, тобто

. (38)

Чим більше значення коефіцієнта детермінації (чим ближче воно до 1) тим більш вагомим і систематичним є вплив пояснюючих змінних на залежну і тим більше підстав стверджувати, що саме зміною значень пояснюючих змінних пояснюється змінна значення залежної змінної моделі, а не іншими випадковими і неврахованими у моделі випадковими факторами. Іншими словами високе, близьке до 1 значення коефіцієнта детермінації свідчить про високий рівень адекватності оціненої моделі статистичним даним.

І навпаки, чим менше значення коефіцієнта детермінації (чим ближче воно до 0) тим менш вагомим є вплив пояснюючих змінних на залежну і тим менше підстав стверджувати, що саме зміною значень пояснюючих змінних пояснюється змінна значення залежної змінної моделі, а не іншими випадковими і неврахованими у моделі випадковими факторами. Іншими словами низьке, близьке до 0 значення коефіцієнта детермінації свідчить про низький рівень адекватності оціненої моделі статистичним даним.

У граничному випадку, коли статистична лінійна залежність між економічними показниками перетворюється на однозначну, функціональну лінійну залежність. При цьому, для парної лінійної регресії всі точки діаграми розсіювання „лягають” на пряму регресії. При варіація значень залежної змінної взагалі не залежить від варіації значень пояснюючих змінних моделі, а пояснюється тільки впливом випадкових факторів. У цьому випадку пояснюючі змінні не мають систематичного впливу на залежну змінну моделі і між економічними показниками відсутній лінійний кореляційно-регресійний зв’язок – тобто побудована модель взагалі не відповідає статистичним даним і слід переглянути її специфікацію.

Як інтерпретується значення коефіцієнта детермінації? Нехай для деякої вибіркової моделі коефіцієнт детермінації дорівнює . Це означає, у даному випадку, що зміна значення залежної змінної моделі на 89% пояснюється зміною значень пояснюючих змінних моделі, а на 11% - іншими випадковими факторами. Таким чином вплив пояснюючих змінних на залежну є достатньо суттєвим, що свідчить про високий рівень адекватності моделі статистичним даним.