Передумови застосування методу найменших квадратів (1МНК) - умови Гауса-Маркова.

Теорема Гауса – Маркова показує, що якщо виконуються усі основні припущення класичного лінійного регресійного аналізу, розглянуті вище, то оцінки параметрів моделі, отримані 1МНК є BLUE – оцінками, тобто найкращими незміщеними лінійними оцінками (best linear unbiased estimators) і мають наступні властивості.

1. Вони є незміщеними оцінками, тобто оцінками, які задовольняють умові

. (22)

Незміщеність оцінки означає, що при багаторазовому повторені випадкової вибірки попри те, що для окремих вибірок, можливо будуть помилки оцінювання, середнє значення цих помилок дорівнює нулю.

2. Вони є ефективними, тобто ці оцінки мають найменшу дисперсію серед усіх незміщених оцінок, отриманих іншими методами.

3. Вони є обгрунтованими оцінками, тобто оцінками, які при довільному задовольнить умові

. (23)

Обгрунтованість оцінок означає, що чим більше вибірка, тим більше ймовірність того, що помилка оцінки не перевищуватиме достатньо малої напере заданої величини . Іншими словами, при збільшені розміру вибірки зростає надійність обчислених оцінок.

Для визначення емпіричного вектора необхідно використати метод найменших квадратів (МНК), а для цього потрібно, щоб виконувалися певні умови, які називаються умовами Гаусса-Маркова, а саме:

1. Математичне сподівання випадкових відхилень повинно дорівнювати нулеві:

(2.37)

Ця умова вимагає, щоб випадкові відхилення в середньому не впливали на залежну змінну Y, тобто в кожному конкретному спостереженні відхилення може набувати додатні або від’ємні значення, але не повинно спостерігатися систематичне зміщення відхилень в переважній більшості в бік одного знаку.

Із врахуванням вищесказаного, використовуючи рівняння (2.32), будемо мати:

(2.38)

2. Дисперсія випадкових відхилень повинна бути сталою величиною

,

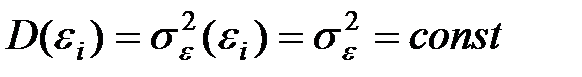(2.39)

Ця вимога передбачає, що не зважаючи на те, що при кожному конкретному спостереженні випадкове відхилення може виявитися відносно великим чи малим, це не повинно складати основу для апріорної причини, тобто причини, що не базується на досвіді, що спонукала б велику похибку.

3. Випадкові відхилення та , повинні бути незалежними одне від одного.

Виконання цієї умови припускає, що між будь-якими випадковими відхиленнями відсутній систематичний зв’язок, тобто величина та знак будь-якого випадкового відхилення не буде являтися причиною величини та знаку будь-якого іншого випадкового відхилення. Цю умову можна записати так

(2.40)

Тут є математичний запис коваріаційного (кореляційного) моменту.

4. Випадковий вектор відхилень повинен бути незалежним від регресорів матриці .

Ця умова виконується автоматично, коли пояснюючі змінні не є стохастичними величинами в заданій моделі.

(2.41)

бо , а 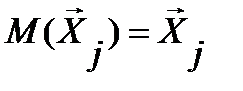( не є випадковою величиною).

5. Компоненти 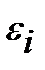випадкового вектора повинні мати нормальний закон розподілу .

Тоді випадковий вектор буде мати нормальний закон розподілу виду .

6. Між регресорами , матриці Х повинна бути відсутня лінійна (кореляційна) залежність. Для цього випадку повинна виконуватися умова.

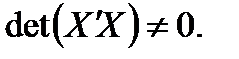
(2.42)

Слід при цьому наголосити, що матриця є симетричною.

7. Економетричні моделі повинні бути лінійними відносно своїх параметрів.

Класичні лінійні моделі	економетричні моделі, для яких виконуються умови (1-7)
Гомоскедастичні моделі	моделі, для яких виконується умова (2) (сталість дисперсії випадкових відхилень)
Гетероскедастичні моделі	моделі, для яких не виконується умова (2) ()

Слід також зауважити, що ранг матриці Х повинен бути

(2.43)

Виконання перелічених умов дає нам право на використання МНК для визначення статистичних оцінок параметрів теоретичної лінійної множинної регресії, перевірку статистичних гіпотез та побудови інтервальних статистичних оцінок.