
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Мета роботи. Вивчення принципів параметричного підсилення
|
|
Вивчення принципів параметричного підсилення. Дослідження одноконтурного параметричного підсилювача.
2 Ключові положення
2.1 Елемент називається параметричним, якщо параметр, що його описує, змінюється в часі. Електричне коло, в якому є хоча б один параметричний елемент, називається параметричним. У радіотехнічних колах знайшли застосування наступні параметричні елементи: резистори – змінюється опір R (t); конденсатори – змінюється ємність C (t); індуктивні елементи – змінюється індуктивність L (t).
Керована зміна параметра дозволяє здійснювати різні перетворення сигналів: підсилення, перетворення частоти, детектування. Особливо ефективні у використанні параметричні підсилювачі – вони характеризуються малим рівнем власних шумів.
 2.2 Одноконтурний параметричний підсилювач виконується на основі коливального контуру, в якому замість звичайної ємності використовується параметрична C (t) (рис. 1). Тут: r – опір втрат контуру; R н – опір навантаження підсилювача. Підсилюваним сигналом є гармонічне коливання
2.2 Одноконтурний параметричний підсилювач виконується на основі коливального контуру, в якому замість звичайної ємності використовується параметрична C (t) (рис. 1). Тут: r – опір втрат контуру; R н – опір навантаження підсилювача. Підсилюваним сигналом є гармонічне коливання
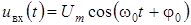 , (1)
, (1)
де w0 і j0 – частота і початкова фаза сигналу.
Частота w0 збігається з резонансною частотою контуру при відсутності зміни ємності, тобто w0 =  .
.
2.3 Зміна ємності описується залежністю
 , (2)
, (2)
де С 0 – середнє значення ємності;
m =D С / С 0 – коефіцієнт зміни (глибина модуляції) ємності;
D С – максимальне прирощення ємності;
wн і jн – частота і початкова фаза накачки.
Параметрична ємність змінюється під впливом керуючого коливання, що поступає від генератора накачки.
2.4 Як параметричний конденсатор найчастіше використовується варикап. Диференціальна ємність p - n переходу варикапа (рис. 2) залежить від величини прикладеної до переходу напруги зворотної полярності и:
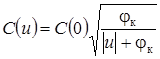 , (3)
, (3)
де С (0) – диференціальна ємність при u = 0 В;
jк – контактна різниця потенціалів порядку 0, 3 В.
 Числові значення С (0) і jк залежать від кристалу, домішок, технології виготовлення та конструкції варикапа.
Числові значення С (0) і jк залежать від кристалу, домішок, технології виготовлення та конструкції варикапа.
2.5 Розглянемо процес обміну енергією між генератором накачки і контуром. Енергія, яка запасена в ємності С, визначається
 , (4)
, (4)
де q = Cu (5)
– заряд на ємності.
Якщо збільшувати ємність без зміни заряду, то зменшується запасена в ній енергія і навпаки. Отже, ємність може віддавати і накопичувати енергію. У випадку параметричної ємності має місце перекачка енергії від джерела керуючого коливання, яке викликало зменшення ємності, та перекачка енергії до джерела керуючого коливання, яке викликало збільшення ємності.
Для більшої наочності процесів, що мають місце в коливальному контурі з параметричною ємністю, будемо вважати, що значення ємності змінюються за законом меандра частоти wн = 2w0. Фаза коливання C (t) вибрана так, що ємність зменшується від C max до C min в моменти часу, коли напруга коливань на контурі приймає амплітудні значення, як показано на рис. 3.
 У момент часу t 1 параметрична ємність зменшується на 2D С = C max – C min. Оскільки заряд ємності не може різко змінитись, то напруга на ємності в момент t 1 збільшується до значення U 1.
У момент часу t 1 параметрична ємність зменшується на 2D С = C max – C min. Оскільки заряд ємності не може різко змінитись, то напруга на ємності в момент t 1 збільшується до значення U 1.
У момент часу t 2 параметрична ємність збільшується на 2D С. Напруга на ємності в момент t 2 повинна була б зменшитись, але в момент t 2 миттєве значення напруги на ємності дорівнює нулю, і зміна ємності не викликає ніяких змін напруги.
Оскільки амплітуда вільних коливань на контурі зменшується відповідно до залежності 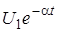 , то в момент часу t 3 напруга на контурі набуває значення
, то в момент часу t 3 напруга на контурі набуває значення  , де a = r /(2 L) – коефіцієнт послаблення контуру; Т 0 = 2p/w0 – період коливань у контурі. У момент часу t 3 параметрична ємність зменшується на 2D С, а напруга на ємності в момент t 3 збільшується до значення U 3. Оскільки збільшення напруги пропорційне зменшенню ємності (5), то
, де a = r /(2 L) – коефіцієнт послаблення контуру; Т 0 = 2p/w0 – період коливань у контурі. У момент часу t 3 параметрична ємність зменшується на 2D С, а напруга на ємності в момент t 3 збільшується до значення U 3. Оскільки збільшення напруги пропорційне зменшенню ємності (5), то
 . (6)
. (6)
З останнього виразу видно, що за рахунок вибору коефіцієнта m можна досягти різних співвідношень між U 1 і U 3. Так, якщо U 3 > U 1, то амплітуда коливання на контурі буде наростати, якщо ж U 3 < U 1, то амплітуда коливання на контурі буде спадати. Критичний коефіцієнт m кр, за якого U 3 = U 1, визначається
 . (7)
. (7)
Із розглянутого явища накачки коливального контуру енергією від джерела накачки випливає, що слід розглядати 2 випадки:
– коефіцієнт m < m кр – накачка коливального контуру еквівалентна зменшенню втрат в контурі (збільшенню добротності), тобто має місце підсилення.
– коефіцієнт m > m кр – амплітуда коливань на контурі може зростати теоретично до нескінченості, а практично до того часу, поки напруга не викличе відкривання варикапа, що призведе до зростання втрат і стабілізації амплітуди коливань на контурі – це генерація коливання.
2.6 Практичний інтерес становить перший випадок. Підкреслимо, що підсилювач повинен працювати в режимі синхронізму підсилюваного сигналу і керуючого коливання. Такий режим роботи одноконтурного параметричного підсилювача називається синхронним. У синхронному режимі частота накачки строго дорівнює подвоєній частоті підсилюваного сигналу:
wн = 2w0. (8)
2.7 Нехай параметрична ємність змінюється відповідно до виразу (2) і виконується умова (8). Тоді схема заміщення параметричної ємності складається із паралельно з’єднаних постійної ємності C 0 і внесеної провідності:
 . (9)
. (9)
 2.8 Заміна параметричної ємності схемою заміщення дозволяє одержати еквівалентну схему одноконтурного параметричного підсилювача. Аналіз зручно вести при паралельному зображенні коливального контуру (рис. 4). Генератор струму i (t) = Im cosw0 t, де Im = Um /r, r = 1/(w0 С 0) – характеристичний опір контуру. Втрати контуру відображені резонансною провідністю G 0 = 1/(r Q) = w0 С 0/ Q. Провідність навантаження G н = 1/ R н. Отже, у синхронному режимі одноконтурний параметричний підсилювач відносно джерела сигналу є колом з постійними параметрами.
2.8 Заміна параметричної ємності схемою заміщення дозволяє одержати еквівалентну схему одноконтурного параметричного підсилювача. Аналіз зручно вести при паралельному зображенні коливального контуру (рис. 4). Генератор струму i (t) = Im cosw0 t, де Im = Um /r, r = 1/(w0 С 0) – характеристичний опір контуру. Втрати контуру відображені резонансною провідністю G 0 = 1/(r Q) = w0 С 0/ Q. Провідність навантаження G н = 1/ R н. Отже, у синхронному режимі одноконтурний параметричний підсилювач відносно джерела сигналу є колом з постійними параметрами.
2.9 Внесена провідність набуває від’ємні значення, коли sin(2j0 – jн) < 0. Якщо
2j0 – jн = – 90°, (10)
то внесена провідність набуває максимальне за модулем значення
G вн = – 0, 5 m w0 C 0. (11)
Внесена провідність компенсує провідність втрат контуру, за рахунок чого і досягається ефект підсилення сигналу. Під коефіцієнтом підсилення параметричного підсилювача прийнято вважати відношення напруги сигналу на навантаженні в схемі з параметричною ємністю до напруги сигналу на навантаженні у схемі без параметричної ємності. Аналіз показує, що при виконанні умов (8) і (10) схема працює як підсилювач, коли  Коли ж
Коли ж  , то підсилювач переводиться в режим генерації. Отже, якщо накачка ємності виконується за гармонічним законом, то критичний коефіцієнт зміни ємності визначається
, то підсилювач переводиться в режим генерації. Отже, якщо накачка ємності виконується за гармонічним законом, то критичний коефіцієнт зміни ємності визначається
m кр = 2/ Q. (12)
Коефіцієнт підсилення
 . (13)
. (13)
2.10 Схема одноконтурного підсилювача має суттєвий недолік – необхідно синхронізувати напругу накачки відносно напруги сигналу. Ця вимога може суттєво ускладнити реалізацію підсилювача або зробити її неможливою. Розглянемо випадок асинхронної накачки, коли wн = 2w0 + Dw, де Dw – довільна частота. Тепер різниця здвоєної початкової фази сигналу і початкової фази накачки у співвідношенні (9) буде визначатись
Ф(t) = 2j0 – Dw t – jн. (14)
Відповідно до виразу (9), внесена за рахунок накачки провідність буде функцією часу
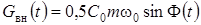 . (15)
. (15)
Вираз для коефіцієнта підсилення тепер є також функцією часу
 . (16)
. (16)
Через залежність коефіцієнта підсилення від часу (16), сигнал буде отримувати додаткову амплітудну модуляцію коливанням KU (t), тобто буде спотворення амплітуди сигналу, що підсилюється. Коливання KU (t) – періодичне, основна частота якого (перша гармоніка) дорівнює Dw. За рахунок додаткової амплітудної модуляції в спектрі сигналу будуть складові частот w0 ± k Dw, k = 1, 2, … Якщо смуга частот сигналу, що підсилюється, не виходить за межі інтервалу (w0 – Dw, w0 + Dw), то смуговим фільтром з граничними частотами смуги пропускання w0 – Dw і w0 + Dw можна виділити корисний сигнал і позбавитись від додаткової амплітудної модуляції коливанням KU (t). При цьому коефіцієнт підсилення сигналу KU буде відповідати середньому значенню KU (t). Проблемно отримати коефіцієнт підсилення хоча б KU = 2. Якщо ж врахувати, що коефіцієнт передачі смугового фільтра менше одиниці, то розглянута ідея асинхронної накачки мало корисна.
Через виявлений недолік (необхідність синхронізації підсилюваного сигналу і коливання накачки) одноконтурні підсилювачі не одержали широкого поширення. Однак уявлення про явища, що відбуваються в одноконтурному підсилювачі, необхідні для розуміння принципів побудови інших більш досконалих параметричних підсилювачів, зокрема, двоконтурних.
3 Ключові питання
3.1 Дати визначення параметричного елемента і параметричного кола. Навести приклади параметричних елементів.
3.2 Як виконати параметричний конденсатор на основі варикапу?
3.3 Зобразити схему одноконтурного параметричного підсилювача.
3.4 Пояснити принцип параметричного підсилення.
3.5 Дати визначення синхронного та асинхронного режимів роботи одноконтурного параметричного підсилювача.
3.6 Що таке внесена в контур провідність, від яких параметрів вона залежить?
3.7 Що таке критичний коефіцієнт зміни параметричної ємності?
3.8 Що таке коефіцієнт підсилення параметричного підсилювача?
3.9 Записати вираз для коефіцієнта підсилення в синхронному режимі.
3.10 Назвати причину, за якої одноконтурний параметричний підсилювач не знайшов широкого застосування.
4 Домашнє завдання
4.1 Вивчити розділ “Перетворення сигналів в лінійних параметричних колах” за конспектом лекцій і літературою [1, с. 299…314; 2, с. 314…320].
4.2 Розрахувати дві залежності коефіцієнта підсилення одноконтурного параметричного підсилювача від коефіцієнта зміни ємності m для діапазону значень 0 £ m < m кр: перша залежність для 2j0 – jн = –90°; друга залежність для 2j0 – jн = –90°+ N × 30°, де N – номер лабораторного стенда. Добротність контуру Q = 40. Режим роботи підсилювача синхронний.
Побудувати графік залежності коефіцієнта підсилення від фази Ф(t) за формулою (16), якщо m = (1 – N × 0, 05)× m кр. Під час розрахунку фаза Ф(t) змінюється на інтервалі (–180°, 180°).
4.3 Підготуватись до обговорення за ключовими питаннями.