Раздел 1. СТАТИКА

Задача 1. Груз весом Р = 60 кН подвешен при помощи каната, перекинутого через небольшой блок А и идущего к лебедке D. Определить усилия в стержнях АС и ВА крана. Углы, определяющие направления стержней и каната, заданы на рис. 1.

.

Рис. 1

Решение. Рассмотрим равновесие узла А крана, к которому приложены сила Р, реакции стержней АС и АВ и сила натяжения каната AD. Обозна­чим реакцию стержня АВ через S ₁ реакцию стержня АС через S ₂ и силу натяжения каната AD через Т.

Реакции стержней S ₁ и S ₂ направим вдоль этих стержней от узла А; сила Т направлена, очевидно, вдоль каната от А к D, так как канат растянут. Кроме того, Т=Р, так как при отсутствии трения в блоке натяжение каната, перекинутого через этот блок, во всех точках одинаково.

Так как узел А находится в равновесии под действием сил S ₁, S ₂, P, Т, то можно составить два уравнения равновесия этой системы сходящихся сил.

Выберем оси координат, как указано на рис. 1, найдем проекцию каждой силы на эти оси и составим два уравнения равновесия, приравнивая нулю сумму проекций всех сил на каждую из координатных осей:

Из второго уравнения находим:

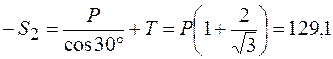кН,

S ₂ =-129, 1 кН.

Теперь из первого уравнения получаем:

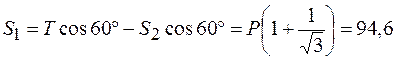кН.

Так как полученное значение силы S ₂ отрицательно, то сила S ₂ имеет направление, противоположное направлению, выбранному на рисунке, т.е. она направлена от С к А, и, следовательно, стержень АС сжат.

Задачу можно решить и геометрически, построив замкнутый многоугольник сил Т, Р, S ₁, S ₂ (рис. 2).

Рис. 2

Направления сил S ₁ и S ₂ найдем после того, как обойдем периметр построенного силового многоугольника, причем направ­ление этого обхода определяется направлением известных сил Р и Т.

Измерив стороны cd и da силового многоугольника выбранной единицей масштаба, найдем величину искомых сил S ₁ и S ₂. Так как углы между силами Т, Р, S ₁, S ₂ заданы, то можно найти углы силового многоугольника, а затем вычислить и длины двух неизвестных его сторон. В самом деле, из построения силового многоугольника следует, что

,

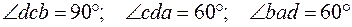а потому

.

Если соединим точки а и с, то треугольник аbс будет равно­бедренным, так как Р = Т, а потому

.

Отсюда следует, что

.

Применяя теперь к треугольнику adc теорему синусов, получим:

,

откуда

,

.

Чтобы определить, будут ли стержни АВ и АС сжаты или растянуты (рис. 2), перенесем векторы S ₁ и S ₂ с силового многоугольника на стержни АВ и АС, тогда сила S ₂ будет направлена к узлу А, а сила S ₁, от узла А, а потому стержень АС сжат, а стержень АВ растянут.

Задача 2. На балку с защемленным концом (рис. 3, а) действует распределенная по линейному закону нагрузка интенсивностью q = 0, 2 кН/м. Сила F = 10 кH действует под углом α = 45⁰ к оси балки, кроме того, приложена пара сил с моментом М = 4 кH∙ м. Определить реакцию заделки.

Решение. 1. Составление расчетной схемы (рис. 3, б). Объектом равновесия является балка АВ. К ней приложены активные силы , пара сил с моментом ираспределенная по линейному закону нагрузка. Равнодействующая приложена в точке О,

Связью, наложенной на балку АВ, является жесткая заделка А. Применяя принцип освобождаемости от связей к балке АВ, заменим действие этой заделки на балку силами реакций и реактивным моментом . Рассмотрим теперь равновесие балки АВ как свободного твердого тела, на которое действуют, кроме активных сил, еще и реакции связи.

2. Условия равновесия:

.

3. Составление уравнений равновесия. Для плоской произвольной системы сил условиям равновесия соответствуют три уравнения:

; (а)

; (б)

. (в)

Для балки с жёсткой заделкой в качестве моментальной точки лучше брать заделку, что позволит исключить лишние неизвестные.

4. Определение искомых величин, проверка правильности решения и анализ полученных результатов.

Из уравнения (а) находим:

.

Из уравнения (б) получаем:

.

Наконец, из уравнения (в) находим:

Проверка. Составим уравнение моментов относительно точки В, подставим найденные реакции:

.

Положительные значения реакций связей подтверждают правильность выбранных направлений этих сил.

Задача 3. Найти реакции опор конструкции (рис. 4, а) при сле­дующих данных: G = 40 кН; Р = 5 кН; М = 10 кНм; q = 2, 5 кН/м; α = 30°; размеры - в м.

Рис. 4

Решение. Рассмотрим систему сил, приложенных к балке АВ. Отбрасываем связи: шарнирно неподвижную опору А, стержень CD и нить.

Действие связей заменяем их реакциями (рис. 4, б). Так как на­правление реакции шарнирно-неподвижной опоры А неизвестно, то определяем ее составляющие Х_А и Y_A.

Покажем также реакцию S_CD стержня CD и реакцию S нити. Модуль этой реакции равен Р. Равномерно распределенную нагруз­ку интенсивностью q заменяем сосредоточенной силой Q, равной q = 5 кН и приложенной в центре тяжести эпюры этой нагрузки.

Для плоской системы сил, приложенных к балке, составляем три уравнения равновесия:

(2.1)

(2.2)

. (2.3)

Из уравнения (2.1) получаем

Из уравнения (2.2)

.

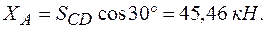Из уравнения (2.3)

.

Вывод: Значения Х_А, Y_A, S_СD получились положительными. Это указыва­ет на то, что принятые направления этих сил совпадают с их дейст­вительными направлениями.

Задача 4.. Горизонтальный вал весом G = 15 Н может вращаться в цилиндрических шарнирах А и В (рис. 5). К шкиву 1 приложено нормальное давление N и касательная сила сопротивления F = 0, 1 N.

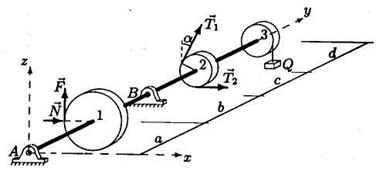
Рис. 5

На шкив 2 действуют силы натяжения ремней Т_г = 30 Н, Т ₂ = 57 Н. Груз Q = 18 Н висит на нити, навитой на шкив 3. Определить силу давления N и реакции шарниров в условии равновесия вала. Учесть веса шкивов: Р_г = 35 Н, Р ₂ = 10 Н, Р ₃ = 15 Н. Все нагрузки действуют в вертикальных плоскостях. Известны радиусы шкивов, R ₁= 26 см, R ₂ = 10 см, R ₃ = 11 см и расстояния между характер­ными точками вала: а = 22 см, b = 25 см, с = 26 см, d = 26 см. Общая длина вала L = a + b + c + d; α =30°.

Рис. 6