Раздел 3. Динамика

Задача 1. Груз 3 массы т поднимается по наклонной плоско­сти, образующей с горизонтом угол , при помощи лебедки, со­стоящей из пары зубчатых колес 7, 2 и барабана радиуса r ₂ (рис. 1). Колесо 1 приводится во вращение электромотором. Барабан жестко скреплен с колесом 2. Определить натяжение троса, пренеб­регая его деформацией, если колесо 1 вращается с угловым ускоре­нием . Радиусы колес R ₁ и R ₂. Коэффициент трения груза о плос­кость равен f. Массой троса пренебречь.

Рис. 1

Решение. Определим ускорение груза. Поскольку деформацией троса пренебрегаем, то

,

где - угловое ускорение барабана.

Однако

,

поэтому

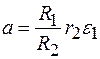. (10.8)

Полагая груз материальной точкой, освободим его от связей, за­менив их действие силами реакции. Изобразим силы, действующие m груз (рис. 2): силу тяжести , реакцию троса , нормальную реакцию плоскости и силу трения .

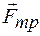Составим дифференциальные уравнения движения груза в про­екциях на оси координат:

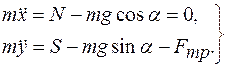(10.9)

Из первого уравнения . Следовательно,

.

Рис. 2

Из второго уравнения систе­мы (10.9)

.

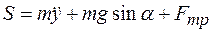Подставляя сюда значение силы трения и учитывая, что (10.8), получаем

.

Натяжение троса численно равно реакции S.

Задача 2. В железнодорожных скальных выемках для защиты кюветов от попадания в них с откосов каменных осыпей устраивается «полка» DC. Учитывая возможность движения камня из наивысшей точки А откоса и полагая при этом его начальную скорость , определить наименьшую ширину полки b и скорость , с которой камень падает на нее. По участку АВ откоса, составляющему угол α с горизонтом и имеющему длину l, камень движется τ с. Коэффициент трения скольжения f камня на участке АВ считать постоянным, а сопротивлением воздуха пренебречь.

Дано: . Определить b и (рис. 3).

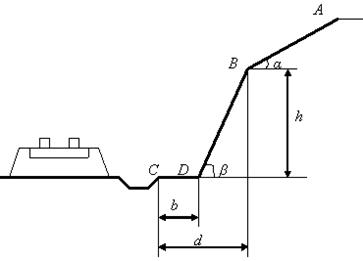
Рис. 3

Решение. Задачу разделим на два этапа. Первый – движение камня на участке АВ, второй – движение камня от точки В до С.

Первый этап. 1. Составление расчетной схемы. Ось проводим по направлению движения камня, ось - перпендикулярно к оси . Камень принимаем за материальную точку и показываем ее в текущем положении, изображаем действующие на камень (точку) силы: вес , нормальную реакцию и силу трения скольжения 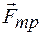(рис. 4).

2.Выявление начальных условий.

При .

Рис. 4

3.Составление дифференциальных уравнений движения точки. Так как точка (камень) движется прямолинейно, то при направлении оси х вдоль траектории получим одно дифференциальное уравнение движения

;

сила трения

,

тогда

;

;

.

4.Интегрирование дифференциальных уравнений движения. Интегрируя дифференциальное уравнение дважды, получаем:

;

;

;

;

;

;

.

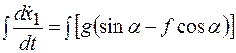5.Определение постоянных интегрирования. Подставим начальные условия, т.е. в уравнения:

;

;

.

6.Нахождение неизвестных величин и исследование полученных результатов. После подстановки постоянных интегрирования С ₁ и С ₂ получаем уравнение скорости и уравнение движения:

;

.

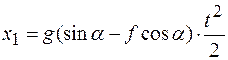Для момента времени τ, когда камень покидает участок АВ,

,

т.е.

;

.

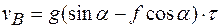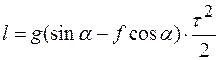Умножим первое уравнение на τ / 2, после этого разделим его на второе. В результате получим:

; ;

.

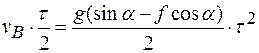Второй этап. Движение камня от точки В до точки С.

1.Составление расчетной схемы. Координатные оси покажем так, как это удобно для решения задачи, в нашем случае ось х параллельна горизонтали и проходит через точку В, ось у направляем вниз через точку В. Камень принимаем за материальную точку, показываем ее в текущем положении, изображаем действующую на камень силу тяжести (рис. 10.4).

2. Выявление начальных условий движения. При :

.

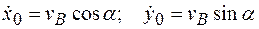3.Составление дифференциальных уравнений движения. Так как движение точки происходит в плоскости ху, то число уравнений движения равно двум:

.

4.Интегрирование дифференциальных уравнений движения. Интегрируем дифференциальные уравнения дважды:

(a)

; (б)

(в)

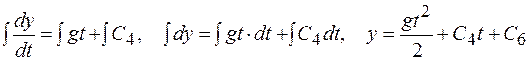. (г)

5. Определение постоянных интегрирования. Подставляем начальные условия: в уравнения (а – г):

,

откуда

.

6.Нахождение искомых величин и исследование полученных результатов. После подстановки постоянных интегрирования в уравнения (а –г) получаем следующие уравнения проекций скорости камня:

и уравнения его движения

.

Уравнение траектории камня найдем, исключив параметр t из уравнений движения:

;

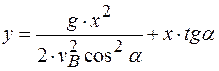– уравнение параболы.

В момент падения . Определим d из уравнения траектории:

; ;

.

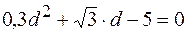Так как траекторией движения камня является ветвь параболы с положительными абсциссами ее точек, то d =2, 11 м.

Минимальная ширина полки

.

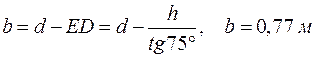Используя уравнение движения камня 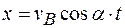, найдем время Т движения камня от точки В до точки С

.

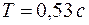Скорость камня при падении найдем через проекции скорости на оси координат:

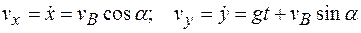
по формуле

.

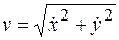Для момента падения t=T= 0, 53 c

.

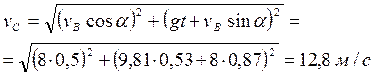Скорость камня при падении равна 12, 8 м/с.

Задача 3. Определить дав­ление на подшипник О, если груз 1 опускается с ускорением а ₁ (рис. 5). Массы тел равны т ₁, т ₂, т ₃, радиусы ступеней блока R и r. Массу нити и сопротивление движению не учитывать. Центр масс блока совпадает с точкой О.

Рис. 5

Решение. Определение дав­ления на подшипник О заменим определением реакции подшип­ника, так как эти силы имеют равные величины. Внешними си­лами, действующими на систему, являются силы тяжести и реакции подшип­ника . Для определения реакций подшипника воспользуемся теоремой о движении центра масс в проекциях на координатные оси

В рассматриваемом случае

откуда

(11.10)

Таким образом, для определения реакций подшипника необхо­димо знать проекции ускорения центра масс системы на координат­ные оси.

По определению центра масс

,

где проекции ускорений центров масс тел системы на координатные оси

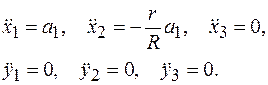
Здесь учтено, что 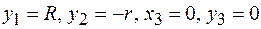; следовательно,

.

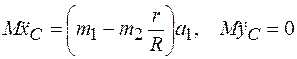Подставляя последние формулы в (11.10), получаем

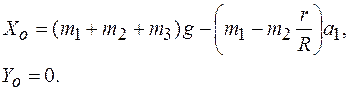
Таким образом, давление на подшипник О определяется по формуле

в которой слагаемое, подчеркнутое одной линией, равно статиче­скому давлению, а слагаемое, подчеркнутое двойной линией, опре­деляет дополнительное давление, зависящее от движения системы.

Задача 4. Шкив массой т = 90 кг и радиусом r = 30 см враща­ется с угловой скоростью ω = 20 с ^–1. Для его остановки на шкив оказывается действие через невесомый ремень, натяжения ветвей которого равны Т ₁= 40 Н и Т ₂ = 20 Н (рис. 55). Радиус инерции шкива ρ = 20 см. Определить время торможения шкива t ₁ и угол φ ₁, на который он повернется за это время.

Рис. 55 Рис. 56

Решение. Рассмотрим все силы, действующие на шкив и прилежащую к нему часть ремня: силы натяжения вет­вей ремня Т ₁ и Т ₂, силу тяжести шкива G, составляющие реакции в подшипниках Х ₀ и У ₀ (рис. 56). Применим к шкиву дифференциальное уравнение вращательного движения относительного его оси z

.

Здесь 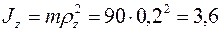кгм ² — осевой момент инер­ции шкива. Стоящий в правой час­ти уравнения главный момент вне­шних сил относительно оси враще­ния обозначим для краткости . Он будет в данном случае равен Нм, по­скольку силы G, Х ₀ и У ₀ имеют ну­левые моменты относительно оси z (моменты сил, действующих по дви­жению, должны браться со знаком «плюс», а против движения — со знаком «минус»).

Таким образом, дифференциальное уравнение враща­тельного движения имеет вид

Для интегрирования этого уравнения делим переменные, учитывая что = const и J_z = const

, (*)

после чего в левой и правой частях ставим интегралы — определенные или неопределенные.

Рассмотрим оба способа решения.

1. Если использовать неопределенные интегралы, по­лучим

,

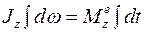oткуда

,

где постоянная интегрирования C ₁ может быть найдена из начального условия ω = ω ₀ при t = 0. Подставив в уравне­ние эти значения, получим 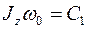J _z, и тогда J_z, откуда

.

2. Если в уравнении (*) использовать определенные интегралы, можно записать

.

Здесь нижние пределы интегралов соответствуют началь­ному моменту времени ω = ω ₀ при t = 0, а верхние — про­извольному моменту времени t и некоторой угловой скорости ω в этот момент времени.

Из последнего уравнения, интегрируя, находим , после чего делаем подстановки , откуда имеем

.

Получили то же решение, что и при первом способе.

Используя последнее соотношение, можно найти вре­мя торможения шкива, т. е. время t _l за которое угловая скорость обратится в ноль

и тогда

Для определения угла поворота φ, заменив в уравнении для угловой скорости ω =d φ /d t, получим

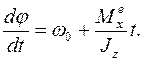
Деля здесь переменные и интегрируя с использованием определенных интегралов (учиты­вая, что φ = 0 при t = 0), находим

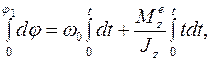
откуда

.

Окончательно имеем рад, что соответствует числу N оборотов шкива: 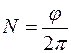= 19, 1 оборотов.

Задача 5. Грузоподъемная установка (рис. 59) состоит из бараба­на с осевым моментом инерции J = 4 кгм ² и радиусом r = 20 см, невесомого и нерастяжимого троса и груза мас­сой т = 103 кг, перемещающегося по наклонной плоско­сти, составляющей угол α = 30° с горизонтом, с коэффи­циентом трения f = 0, 2. Определить величину вращающе­го момента М, который необходимо приложить к барабану, чтобы его угловое ускорение было равно ε = 5 с ^–2.

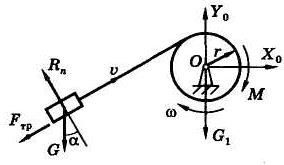
Рис. 59 Рис. 60

Решение. Поскольку рассматривается мгновенное со­стояние системы, то следует применить теорему об изме­нении кинетической энергии в дифференциальной форме

.

При условии, что трос нерастяжим и отсутствует про­скальзывание троса относительно барабана, система явля­ется неизменяемой (внутренние силы не работают), и тог­да производная от кинетической энергии будет опреде­ляться только мощностями внешних сил:

.

Кинетическая энергия системы (поступательно движу­щийся груз и вращающийся барабан, рис. 60)

.

Кинематическая связь, наложенная на скорость груза и угловую скорость барабана, определяется условиями нерастяжимости троса и отсутствием проскальзывания троса относительно барабана: v = ω r. Тогда

.

Выражение в скобках называется приведенным (к ба­рабану) моментом инерции: кгм ².

Итак, кинетическая энергия системы

,

а производная от нее по времени

.

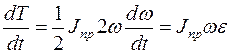дает левую часть записи теоремы.

Рассмотрим действующие в системе внешние силы и их мощности. Сила тяжести барабана G ₁ и составляющие реакции на его оси Х ₀ и Y ₀ будут иметь нулевую мощ­ность (так как равна нулю скорость точки их приложе­ния — точки О). Также равна нулю мощность нормальной реакции груза R,,, поскольку она перпендикулярна ско­рости груза.

Ненулевую мощность будут иметь только сила тяже­сти груза G, сила трения F_mp и вращающий момент М:

;

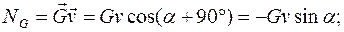Тогда (с учетом кинематической связи) сумма мощно­стей запишется в виде

.

Выражение в квадратных скобках называется приве­денным (к барабану) вращающим моментом: 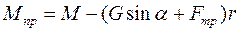, и тогда правая часть записи теоремы имеет вид .

Приравнивая правую и левую части теоремы, получа­ем , отсюда после сокращения находим тре­буемый приведенный вращающий момент

Нм.

Теперь можно найти необходимый вращающий момент: . Учитывая, что , находим .

Задача 6. Рассматривается грузоподъемная установка из преды­дущей задачи. К барабану приложен постоянный вращаю­щий момент М = 3 кНм. Определить угловую скорость барабана после того, как он повернется на угол φ = 10 рад, если движение началось из состояния покоя.

Решение. В постановке данной задачи идет речь о конечном перемещении системы, поэтому следует приме­нить теорему об изменении кинетической энергии в инте­гральной форме:

.

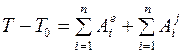Кинетическая энергия системы получена в предыду­щей задаче,

,

где приведенный момент инерции J_np = 44 кгм ². Началь­ная кинетическая энергия системы Т ₀ = 0, так как движе­ние началось из состояния покоя.

Перейдем к вычислению величин работ.

Рис. 61

Внутренние силы в данной системе не работают:

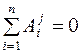
(неизменяемая система), поэтому изменение кинетической энергии будет определяться только работами внешних сил. Внешние силы и соответствующие перемещения показаны на рис. 61 (перемещение груза s и перемещение бара­бана φ).

Сила тяжести барабана G ₁ и составляющие реакции на его оси Х₀ и Y ₀ работы не совершают (так как нет пере­мещения у точки их приложения — точки О). Также равна нулю работа нормальной реакции груза R_n, поскольку она перпендикулярна пере­мещению груза.

Ненулевая работа будет только у силы тяжести груза G, силы трения F_тр и вращающего момента М. Величину этих работ вычисляем по формулам, соответствующим по­стоянным силам и моментам:

.

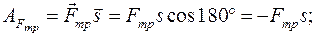
Интегрируя уравнение кинематической связи v = ω r, получаем соотношение для перемещений s = φ r. Тогда сум­марная работа запишется в виде

.

Выражение в квадратных скобках — приведенный вра­щающий момент

Нм,

и тогда правая часть записи теоремы имеет вид

.

Приравнивая правую и левую части теоремы, получаем

,

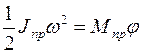откуда искомая угловая скорость

.

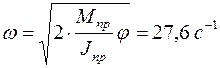Задача 7. Для заданной механической системы определить ускорение груза 1 и натяжение в ветви нити 1, к которой прикреплен груз. Массами нитей пренебречь. Система движется из состояния покоя. Считать, что 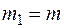, , 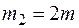, , 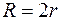см, , f = 0, 1 (рис. 1).

Рис 1

Решение.

1. Составление расчетной схемы. На механическую систему действуют активные силы , , 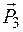. Применяя принцип освобождаемости от связей к внешним связям, покажем , , N. Силу трения изобразим в сторону, противоположную предполагаемую направлению движения.

Рис. 2

Так как система пришла в движение из состояния покоя, то ускорения точек системы 1 направлены в сторону движения.

Приложим силы инерции. Тела 1 и 3 движутся поступательно, силы инерции этих тел выражаются векторами

и показываются на расчетной схеме противоположно ускорениям.

Силы инерции блока 2, вращающегося вокруг неподвижной оси Oz с угловым ускорением , приводятся к паре, момент которой равен

и изображается на схеме в сторону противоположную .