
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Раздел 2. Кинематика
|
|
Задача 1. По заданным уравнениям движения точки М установить вид ее траектории и для момента времени t=0, 5с, найти положение точки на траектории, ее скорость, касательное, нормальное и полное ускорения, а также радиус кривизны траектории (рис. 1):

Рис. 1
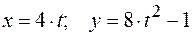 , (2.5)
, (2.5)
где х и у в сантиметрах, t – в секундах.
Решение. Параметрическим представлением траектории является сам закон движения. Уравнение траектории в координатной форме получаем, исключая из закона движения время:
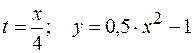 .
.
Получили 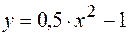 , то есть траекторией точки является парабола. Для построения траектории рассчитаем по уравнениям координаты точек параболы, отвечающие нескольким моментам времени. Результаты расчетов приведены в табл. 2.1.
, то есть траекторией точки является парабола. Для построения траектории рассчитаем по уравнениям координаты точек параболы, отвечающие нескольким моментам времени. Результаты расчетов приведены в табл. 2.1.
Таблица 2.1
| t, с | 0, 5 | ||
| х, cм | |||
| у, см | - 1 |
Траектория построена на рис. 2.24, на ней стрелкой показано направление движения точки из начального положения при  с координатами
с координатами 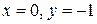 .
.
Дифференцируя (2.5) по времени, находим проекции скорости точки на оси координат х, у:
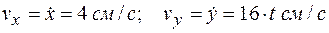 . (2.6)
. (2.6)
При 
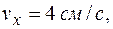
 .
.
По найденным проекциям определяем модуль скорости
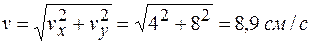 .
.
Дифференцируя (2.6), находим проекции вектора ускорения
 .
.
При 
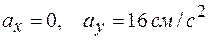 .
.
По найденным проекциям определяем модуль ускорения
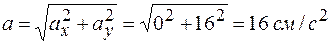 .
.
Определение касательного ускорения при 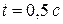
 .
.
Определение нормального ускорения при 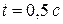
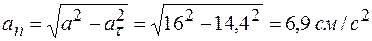 .
.
Определение радиуса кривизны при 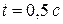
 .
.
Результаты вычислений для заданного момента времени 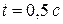 приведены в табл. 2.2.
приведены в табл. 2.2.
Таблица 2.2
| Координаты, см | С к о р о с т ь, см/с | Ус к о р е н и е, см/с 2 | Радиус кривизны, см | |||||||
| х | у | vx | vy | v | ax | ay | a | at | an | r |
| 8, 9 | 14, 4 | 6, 9 | 11, 6 |
На рис. 1 показано положение точки М в заданный момент времени.
Векторы скорости и ускорения точки М построены в масштабе по их проекциям на оси координат:  , там же показаны касательное и нормальное ускорения. Совпадение величин
, там же показаны касательное и нормальное ускорения. Совпадение величин  и
и 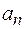 , найденных из чертежа, с их значениями, полученными аналитически, служит контролем правильности решения.
, найденных из чертежа, с их значениями, полученными аналитически, служит контролем правильности решения.
Радиус кривизны проведен в сторону вогнутости траектории перпендикулярно к вектору скорости – по направлению 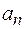 .
.
Задача 2. Лебедка (рис. 2), поднимающая груз по наклонной плоскости, состоит из двух валов 1 л 2 с шестернями (зубчатыми колесами), числа зубьев которых равны соответственно z 1 = 12 и z 2= 48. К валу 2 прикреплен барабан радиусом r= 0, 3 м, на который наматывается грузовой трос. Вал 1 вращается равноускоренно с угловым ускорением ε 1 = 8 с –2. Определить скорость, ускорение и перемещение груза, а также ускорение точки В барабана в момент времени t = 1 с. В начальный момент времени система находилась в покое.
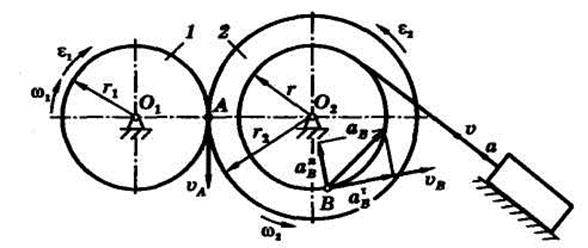
Рис. 2
Решение. Найдем угловую скорость ω 1 ведущего вала 1 из условия, что оно вращается с угловым ускорением ε 1 = const, учитывая, что  . Интегрируя последнее уравнение по времени, получаем
. Интегрируя последнее уравнение по времени, получаем 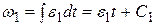 .
.
Постоянную интегрирования получаем из начального условия: при t = 0 ω 1 = 0 (система находилась в покое), следовательно C 1 = 0.
Итак, угловая скорость вала 1 определяется уравнением 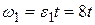 .
.
При t = 1 с получаем  .
.
Шестерни 1 и 2 взаимодействуют без проскальзывания. Поэтому скорости точек их касания (точка А) будут одинаковы:  .
.
Отсюда находим угловую скорость ω 2 вала 2, учитывая, что 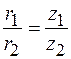 :
:
 .
.
Угловое ускорение вала 2 равно  .
.
Поскольку трос нерастяжим и относительно барабана не проскальзывает, то скорость груза v будет равна скорости любой из точек на ободе барабана, в частности, скорости точки В: v = vB = ω 2 r = 0, 6 t =|t=1 c =0, 6 м/с.
Ускорение точки В равно векторной сумме касательного (вращательного) и нормального (центростремительного) ускорений:  .
.
Направление вращательного ускорения определяется направлением углового ускорения ε 2, а его модуль равен 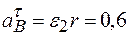 м / с 2. Центростремительное ускорение направлено к оси вращения вала 2 и равно по модулю
м / с 2. Центростремительное ускорение направлено к оси вращения вала 2 и равно по модулю  м / с 2.
м / с 2.
Модуль ускорения точки В
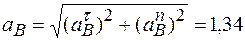 м / с 2.
м / с 2.
Ускорение груза можно найти, взяв производную по времени от его скорости, так как это касательное ускорение:  м / с 2.
м / с 2.
Перемещение груза определяется интегрированием модуля скорости по времени:
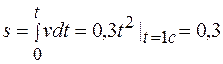 м.
м.
Ответ: v = 0, 6 м/с; а = 0, 6 м/с 2; s = 0, 3 м; аB = = 1, 34 м / с 2.
Задача 3. Кривошип OA длиной 0, 2 м вращается равномерно с угловой скоростью ω OA = 10 с–1 и приводит в движение шатун АВ длиной 1 м. Ползун В движется по вертикали. Найти угловую скорость и угловое ускорение шатуна, а также скорость и ускорение ползуна в момент, когда кривошип и шатун взаимно перпендикулярны и образуют с вертикалью угол 45° (рис. 3).
Решение.
1. Определение скоростей. Вычислим скорость точки А как точки вращающегося кривошипа:
 .
.
Она направлена перпендикулярно ОА (рис. 4).

Рис. 3
Скорость vB ползуна направлена по направляющей вертикально.
Для шатуна АВ, совершающего плоское движение, теперь известны направления скоростей двух его точек: А и В. Восставляя перпендикуляры к векторам этих скоростей, находим точку Р их пересечения — МЦС шатуна.
Используя известную формулу для скоростей точек при плоском движении, получаем 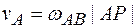 ;
; 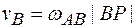 .
.

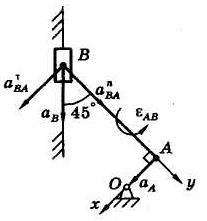
Рис. 4 Рис. 5
Из треугольника АВР имеем | АР | = 1 м; | ВР | = 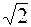 м, и тогда
м, и тогда
 .
.
2. Определение ускорений. Вычислим сначала ускорение точки А как точки кривошипа: 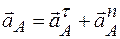 .
.
Здесь вращательное ускорение  , так как
, так как 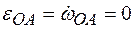 , поскольку
, поскольку 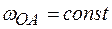 .
.
Тогда полное ускорение точки А равно центростремительному
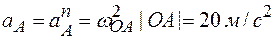
и направлено к оси вращения — точке О (рис. 5).
Для вычисления ускорения точки В воспользуемся теоремой о сложении ускорений, взяв точку А в качестве полюса:
 . (*)
. (*)
Центростремительное ускорение точки В в относительном вращении вокруг точки А по модулю равно  , и направлено от точки В к полюсу — точке А.
, и направлено от точки В к полюсу — точке А.
Модуль вращательного ускорения  определяется по формуле
определяется по формуле  и пока не может быть вычислен, поскольку неизвестна величина углового ускорения
и пока не может быть вычислен, поскольку неизвестна величина углового ускорения 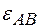 . Направление вектора
. Направление вектора 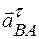 также не может быть определено однозначно, так как неизвестно направление углового ускорения, т. е. неизвестно, ускоренным или замедленным является поворот шатуна. Примем пока этот поворот ускоренным, тогда направление
также не может быть определено однозначно, так как неизвестно направление углового ускорения, т. е. неизвестно, ускоренным или замедленным является поворот шатуна. Примем пока этот поворот ускоренным, тогда направление  совпадет с направлением
совпадет с направлением  , а вектор
, а вектор  направим перпендикулярно отрезку ВА по ходу углового ускорения.
направим перпендикулярно отрезку ВА по ходу углового ускорения.
Вектор ускорения точки В направлен по вертикальной прямолинейной направляющей. Будем пока считать движение ползуна ускоренным и направим ускорение  в ту же сторону, что и скорость
в ту же сторону, что и скорость  (рис. 4, 5).
(рис. 4, 5).
Теперь в равенстве (*) все ускорения имеют определенное направление, и мы можем записать это уравнение в проекциях на выбранные оси:
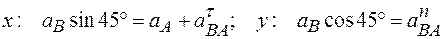 .
.
Из последнего уравнения получаем 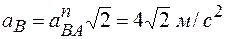 , тогда из первого уравнения
, тогда из первого уравнения
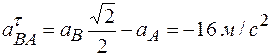 .
.
Отсюда следует, что
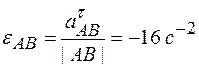 .
.
Отрицательные знаки у величин  и
и 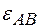 показывают, что их истинные направления противоположны принятым.
показывают, что их истинные направления противоположны принятым.
Задача 4. Тело D вращается в плоскости рисунка (рис. 6) вокруг оси Ох так, что его угол поворота равен
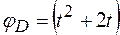 рад.
рад.
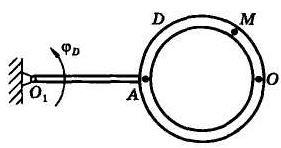
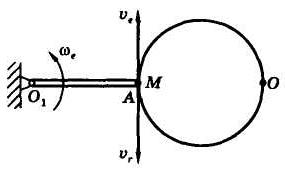
Рис. 6 Рис. 7
По желобу тела ОА движется точка М так, что алгебраическое значение длины дуги равно
ОМ = s = (25 π t 2 – 5 π t) см.
Желоб является окружностью радиусом R = 20 см, расстояние | OA | = b = 10 см. Для момента времени t = 1 с определить абсолютную скорость  и абсолютное ускорение
и абсолютное ускорение 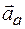 точки М.
точки М.
Решение.
1. Определение  . По теореме о сложении скоростей имеем
. По теореме о сложении скоростей имеем  .
.
Относительную скорость точки (скорость по отношению к телу D) находим, вычисляя ее алгебраическое значение как производную от дуговой координаты по времени: 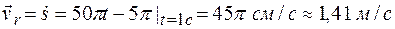 и
и 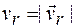 .
.
Чтобы найти ее направление, установим, где находится точка М. При t = 1 с, получив ОМ = 20 π см, устанавливаем, что длина дуги составляет половину длины окружности, то есть точка М находится в точке А желоба (рис. 7).
Скорость 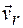 точки направляем по касательной к ее траектории (окружности) в сторону увеличения длины дуги, так как алгебраическое значение скорости положительно.
точки направляем по касательной к ее траектории (окружности) в сторону увеличения длины дуги, так как алгебраическое значение скорости положительно.
Переносной скоростью по определению будет скорость той точки вращающегося тела D, с которой совпадает точка М, то есть скорость точки А:
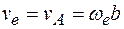 ,
,
где алгебраическое значение угловой скорости переносного движения равно
 .
.
Таким образом, при t = 1 с получаем 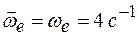 и ve = 0, 40 м/с. Алгебраическое значение угловой скорости положительно, следовательно, вращение происходит по направлению угла поворота. Переносная скорость направлена перпендикулярно отрезку О 1 А по ходу вращения.
и ve = 0, 40 м/с. Алгебраическое значение угловой скорости положительно, следовательно, вращение происходит по направлению угла поворота. Переносная скорость направлена перпендикулярно отрезку О 1 А по ходу вращения.
Поскольку векторы 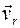 и
и  направлены противоположно, то модуль абсолютной скорости равен va = vr – ve ≈ 1, 01 м/с.
направлены противоположно, то модуль абсолютной скорости равен va = vr – ve ≈ 1, 01 м/с.
2. Определение 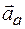 . По теореме Кориолиса
. По теореме Кориолиса  или
или
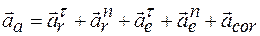 . (*)
. (*)
Вычислим и покажем на рисунке все пять ускорений (рис. 8).
Относительное касательное ускорение вычисляем через его алгебраическое значение:  см / с 2≈ 1, 57 м / с 2.
см / с 2≈ 1, 57 м / с 2.
Ускорение  направлено туда же, куда и скорость
направлено туда же, куда и скорость 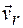 , так как знаки их алгебраических значений совпадают (ускоренное движение):
, так как знаки их алгебраических значений совпадают (ускоренное движение): 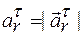 . Относительное нормальное ускорение направлено к центру желоба и равно
. Относительное нормальное ускорение направлено к центру желоба и равно
 м / с 2.
м / с 2.
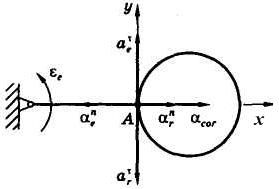
Рис. 8
Переносное ускорение в данном случае — это ускорение точки А тела D.
Так как алгебраическое значение углового ускорения равно его модулю
 ,
,
то переносное вращательное ускорение получается
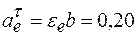 м / с 2.
м / с 2.
Оно направлено перпендикулярно О 1 A по ходу углового ускорения, и поскольку алгебраические значения угловой скорости и углового ускорения совпадают по знаку (ускоренное вращение), следовательно, 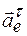 совпадает с
совпадает с 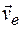 .
.
Переносное центростремительное ускорение направлено к оси О 1 и равно
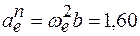 м / с 2.
м / с 2.
Кориолисово ускорение 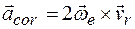 , и его модуль равен
, и его модуль равен
 .
.
Так как вектор угловой скорости тела лежит на оси вращения, то в данном случае он перпендикулярен плоскости чертежа и угол между ним и вектором относительной скорости равен 90°. Тогда 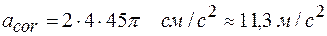 .
.
Направление кориолисова ускорения может быть найдено или по общему правилу для векторного произведения, или по специальному правилу Жуковского. В нашем случае достаточно повернуть скорость 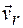 на 90° по ходу вращения тела.
на 90° по ходу вращения тела.
Сложение векторов произведем с помощью проекций. Спроектировав равенство (*) на оси, получим
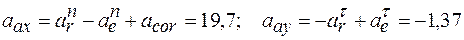
и окончательно
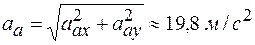 .
.